
【题目】定义在R上的奇函数![]() 满足
满足![]() ,且在[0,1)上单调递减,若方程
,且在[0,1)上单调递减,若方程![]() 在[0,1)上有实数根,则方程
在[0,1)上有实数根,则方程![]() 在区间[-1,7]上所有实根之和是
在区间[-1,7]上所有实根之和是
A. 12 B. 14 C. 6 D. 7
【答案】A
【解析】由f(2-x)=f(x)知函数f(x)的图象关于直线x=1对称,
由f(x)是R上的奇函数知f(2-x)=-f(x-2),f(x-4)=-f(4-x)
在f(2-x)=f(x)中,以x-2代x得:
f(2-(x-2))=f(x-2)即f(4-x)=f(x-2),
所以f(x)=f(2-x)=-f(4-x)=f(x-4)
即f(x+4)=f(x),
所以f(x)是以4为周期的周期函数.
考虑f(x)的一个周期,例如[-1,3],
由f(x)在[0,1)上是减函数知f(x)在(1,2]上是增函数,
f(x)在(-1,0]上是减函数,f(x)在[2,3)上是增函数.
对于奇函数f(x)有f(0)=0,f(2)=f(2-2)=f(0)=0,
故当x∈(0,1)时,f(x)<f(0)=0,当x∈(1,2)时,f(x)<f(2)=0,
当x∈(-1,0)时,f(x)>f(0)=0,当x∈(2,3)时,f(x)>f(2)=0,
方程f(x)=-1在[0,1)上有实数根,
则这实数根是唯一的,因为f(x)在(0,1)上是单调函数,
则由于f(2-x)=f(x),故方程f(x)=-1在(1,2)上有唯一实数.
在(-1,0)和(2,3)上f(x)>0,
则方程f(x)=-1在(-1,0)和(2,3)上没有实数根.
从而方程f(x)=-1在一个周期内有且仅有两个实数根.
当x∈[-1,3],方程f(x)=-1的两实数根之和为x+2-x=2,
当x∈[-1,7],方程f(x)=-1的所有四个实数根之和为x+2-x+4+x+4+2-x=2+8+2=12.
故答案为A.


科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列, ![]() ,
, ![]() ,
, ![]() 判断
判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右有顶点分别是
的左、右有顶点分别是![]() 、
、![]() ,上顶点是
,上顶点是![]() ,圆
,圆![]() :
:![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离是
的距离是![]() ,且椭圆的右焦点与抛物线
,且椭圆的右焦点与抛物线![]() 的焦点重合.
的焦点重合.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)平行于![]() 轴的动直线与椭圆和圆在第一象限内的交点分别为
轴的动直线与椭圆和圆在第一象限内的交点分别为![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与
与![]() 轴的交点记为
轴的交点记为![]() ,
,![]() .试判断
.试判断![]() 是否为定值,若是,证明你的结论.若不是,举反例说明.
是否为定值,若是,证明你的结论.若不是,举反例说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (限定
(限定![]() ).
).
(1)写出曲线![]() 的极坐标方程,并求
的极坐标方程,并求![]() 与
与![]() 交点的极坐标;
交点的极坐标;
(2)射线![]() 与曲线
与曲线![]() 与
与![]() 分别交于点
分别交于点![]() (
(![]() 异于原点),求
异于原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,如图,以C为原点,分别以CA,CB,CC1为x,y,z轴建立空间直角坐标系.
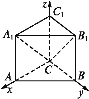
(1)求平面A1B1C的法向量;
(2)求直线AC与平面A1B1C夹角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com