
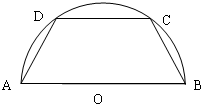
 如图半径为2的圆内接等腰梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
如图半径为2的圆内接等腰梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.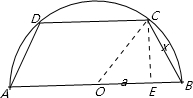
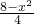 ;
;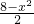 =-
=- +2x+8;由0<a<2,得0<
+2x+8;由0<a<2,得0<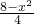 <2,∴0<x<2
<2,∴0<x<2 ;
; ;
; +2x+8=-
+2x+8=- (x-2)2+10,其中x∈(0,2
(x-2)2+10,其中x∈(0,2 ),所以,当x=2时,y有最大值,为10.
),所以,当x=2时,y有最大值,为10. +2x+8是二次函数,定义域为x∈(0,
+2x+8是二次函数,定义域为x∈(0, ),用配方法可以求得y的最大值及对应x的值.
),用配方法可以求得y的最大值及对应x的值.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个圆的面积之和,则
如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个圆的面积之和,则| lim |
| n→∞ |
| A、2πr2 | ||
B、
| ||
| C、4πr2 | ||
| D、6πr2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
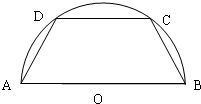 如图半径为2的圆内接等腰梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
如图半径为2的圆内接等腰梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.查看答案和解析>>
科目:高中数学 来源: 题型:
如图4,EFGH是以O为圆心,半径为1的圆内接正方形.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形OHE(阴影部分)内”,则
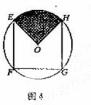
(1)![]() ;(2)
;(2)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图4,EFGH是以O为圆心,半径为1的圆内接正方形.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形OHE(阴影部分)内”,则
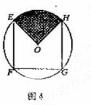
(1)![]() ;(2)
;(2)![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com