
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 是函数
是函数![]() 的极值点,求曲线
的极值点,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的单调区间;
的单调区间;
(3)已知![]() ,当
,当![]() ,试比较
,试比较![]() 与
与![]() 的大小,并给予证明.
的大小,并给予证明.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() ,证明见解析.
,证明见解析.
【解析】
(1)根据极值点定义可构造方程求得![]() ,根据导数几何意义可求得结果;
,根据导数几何意义可求得结果;
(2)分别在![]() 和
和![]() 两种情况下,根据导函数的正负得到原函数的单调区间;
两种情况下,根据导函数的正负得到原函数的单调区间;
(3)令![]() ,可求得
,可求得![]() ;令
;令![]() ,利用导数和零点存在定理可确定
,利用导数和零点存在定理可确定![]() ,即
,即![]() 的正负,从而得到
的正负,从而得到![]() 的单调性和最值,通过最值可知
的单调性和最值,通过最值可知![]() ,进而得到大小关系.
,进而得到大小关系.
(1)由题意得:![]() ,
,
![]() 是
是![]() 的极值点,
的极值点,![]() ,解得:
,解得:![]()
![]() ,又
,又![]() ,
,
![]() 所求切线方程为
所求切线方程为![]() ,即
,即![]() .
.
(2)由题意得:![]() 定义域为
定义域为![]() ,
,![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;
,无单调递减区间;
当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
![]() 的单调递增区间为
的单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;
;
综上所述:当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;当
,无单调递减区间;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(3)令![]() ,
,
则![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 函数
函数![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,![]() 存在唯一零点
存在唯一零点![]() ,使得
,使得![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
![]() 函数
函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,![]() ,
,
又![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,
![]() 在
在![]() 上恒成立.
上恒成立.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》卷第五《商功》中,有“贾令刍童,上广一尺,袤二尺,下广三尺,袤四尺,高一尺。”,意思是:“假设一个刍童,上底面宽1尺,长2尺;下底面宽3尺,长4尺,高1尺(如图)。”(注:刍童为上下底面为相互平行的不相似长方形,两底面的中心连线与底面垂直的几何体),若该几何体所有顶点在一球体的表面上,则该球体的表面积为( )
A. ![]() 平方尺 B.
平方尺 B. ![]() 平方尺 C.
平方尺 C. ![]() 平方尺 D.
平方尺 D. ![]() 平方尺
平方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导数f'(x),x∈R,有f(-x)+f(x)=x2,在(0,+∞)上,f'(x)<x,若f(6-m)-f(m)-18+6m≥0,则实数m的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数在
,那么该函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(1)已知![]() ,利用上述性质,求函数
,利用上述性质,求函数![]() 的单调区间和值域;
的单调区间和值域;
(2)对于(1)中的函数![]() 和函数
和函数![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为了解学生对学校食堂服务的满意度,随机调查了50名男生和50名女生,每位学生对食堂的服务给出满意或不满意的评价,得到如图所示的列联表.经计算![]() 的观测值
的观测值![]() ,则可以推断出( )
,则可以推断出( )
满意 | 不满意 | |
男 | 30 | 20 |
女 | 40 | 10 |
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
A.该学校男生对食堂服务满意的概率的估计值为![]()
B.调研结果显示,该学校男生比女生对食堂服务更满意
C.有95%的把握认为男、女生对该食堂服务的评价有差异
D.有99%的把握认为男、女生对该食堂服务的评价有差异
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.
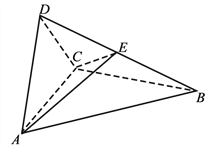
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com