
【题目】已知函数f(x)=ax3+bx在x=2处取得极值为﹣16
(1)求a,b的值;
(2)若f(x)的单调区间.
【答案】
(1)解:函数f(x)=ax3+bx的导数为f′(x)=3ax2+b,
由于f(x) 在x=2处取得极值为﹣16
故有f(2)=﹣16,且f′(2)=0
即12a+b=0且8a+2b=﹣16,
解得a=1,b=﹣12
(2)解:由(1)知 f(x)=x3﹣12x的导数为f′(x)=3x2﹣12,
令f′(x0=0,得x1=﹣2,x2=2,
当f′(x)>0,即x<﹣2或x>2时,函数f(x)为增函数;
当f′(x)<0,即﹣2<x<2时,函数f(x)为减函数.
则f(x)的增区间为(﹣∞,﹣2),(2,+∞),减区间为(﹣2,2)
【解析】(1)求得函数f(x)的导数,由题意可得f(2)=﹣16,且f′(2)=0,解a,b的方程组,即可得到a,b的值;(2)求出f(x)的导数,由导数大于0,可得增区间;导数小于0,可得减区间.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
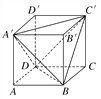
(1)三棱锥A′-BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′-BC′D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() 是定义在[-l,1]上的奇函数,且f(
是定义在[-l,1]上的奇函数,且f(![]() )=
)=![]() 。
。
(1)确定函数f(x)的解析式;
(2)判断并用定义证明f(x)在(-1,1)上的单调性;
(3)若f(1-3m)+f(1+m)≥0,求实数m的所有可能的取值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(其中A>0,ω>0,0<φ<
,(其中A>0,ω>0,0<φ<![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为![]() ,且图象上一个最低点为M(
,且图象上一个最低点为M(![]() ,-2).
,-2).
(1)求f(x)的解析式;
(2)将函数f(x)的图象向右平移![]() 个单位后,再将所得图象上各点的横坐标缩小到原来的
个单位后,再将所得图象上各点的横坐标缩小到原来的![]() ,纵坐标不变,得到y=g(x)的图象,求函数y=g(x)的解析式.
,纵坐标不变,得到y=g(x)的图象,求函数y=g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xex , 则( )
A.x=1为f(x)的极大值点
B.x=1为f(x)的极小值点
C.x=﹣1为f(x)的极大值点
D.x=﹣1为f(x)的极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数),如图所示.据图中提供的信息,回答下列问题:
为常数),如图所示.据图中提供的信息,回答下列问题:

(1)写出从药物释放开始,每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)之间的函数关系式;
(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到![]() 毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?
毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?
查看答案和解析>>
科目:高中数学 来源: 题型:
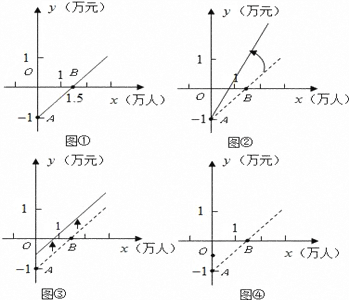
【题目】如图是某公共汽车线路收支差额(票价总收人减去运营成本)与乘客量的函数图象.目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会.乘客代表认为:公交公司应节约能源,改善管理,降低运营成本,以此举实现扭亏.公交公司认为:运营成本难以下降,公司己尽力,提高票价才能扭亏.根据这两种意见,可以把图分别改画成图②和图③,
(1)说明图①中点![]() 和点
和点![]() 以及射线
以及射线![]() 的实际意义;
的实际意义;
(2)你认为图②和图③两个图象中,反映乘客意见的是_________,反映公交公司意见的是_________.
(3)如果公交公司采用适当提高票价又减少成本的办法实现扭亏为赢,请你在图④中画出符合这种办法的大致函数关系图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S—ABCD的底面为正方形,SD⊥底面ABCD,则下列结论
①AC⊥SB
②AB∥平面SCD
③SA与平面ABD所成的角等于SC与平面ABD所成的角
④AB与SC所成的角等于DC与SA所成的角.
⑤二面角![]() 的大小为
的大小为![]()
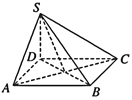
其中,正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
加工零件x(个) | 10 | 20 | 30 | 40 | 50 |
加工时间y(分钟) | 64 | 69 | 75 | 82 | 90 |
经检验,这组样本数据具有线性相关关系,那么对于加工零件的个数x与加工时间y这两个变量,下列判断正确的是( )
A.成正相关,其回归直线经过点(30,75)
B.成正相关,其回归直线经过点(30,76)
C.成负相关,其回归直线经过点(30,76)
D.成负相关,其回归直线经过点(30,75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com