
【题目】已知函数![]() 为偶函数,函数
为偶函数,函数![]() 为奇函数。
为奇函数。![]() 对任意实数x恒成立.
对任意实数x恒成立.
(1)求函数![]() 与
与![]() ;
;
(2)设![]() ,
,![]() ,若
,若![]() 对于
对于![]() 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)对于(2)中的函数![]() ,若方程
,若方程![]() 没有实数解,实数m的取值范围.
没有实数解,实数m的取值范围.
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)
(3)![]() .
.
【解析】
(1)利用函数的奇偶性,列方程组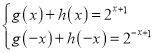 求函数的解析式;
求函数的解析式;
(2)由(1)变形![]() ,由不等式
,由不等式![]() 恒成立,
恒成立,![]() ,参变分离后
,参变分离后![]() 恒成立,转化为求函数
恒成立,转化为求函数![]() 的最大值;
的最大值;
(3)首先讨论![]() 解得情况,当
解得情况,当![]() 时,满足条件,当
时,满足条件,当![]() 时,方程
时,方程![]() 有两个根
有两个根![]() ,
,![]() ,假设
,假设![]() ,由于函数开口向上,故
,由于函数开口向上,故![]() 没有实数解,而
没有实数解,而![]() 的最小值为
的最小值为![]() ,列等价的不等式组求解,当
,列等价的不等式组求解,当![]() 时,
时,![]() ,
,![]() ,
,![]() 时,
时,![]() ,而
,而![]() 无解,满足条件,综上以上三种情况求得
无解,满足条件,综上以上三种情况求得![]() 的取值范围.
的取值范围.
(1)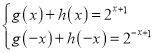 ,
,
![]() 函数
函数![]() 为偶函数,函数
为偶函数,函数![]() 为奇函数
为奇函数
即 ,两式相加得
,两式相加得![]()
![]() ,
,
![]() ;
;
(2)![]()
![]()
![]() ,
,
![]() ,
,
![]() 不等式等价于
不等式等价于![]() 恒成立,
恒成立,![]()
参变分离后![]() 恒成立,
恒成立,
当![]() 时,
时,![]() 是单调递减函数,
是单调递减函数,
![]() 时,函数取得最大值-3,
时,函数取得最大值-3,
即![]() ;
;
(3)首先讨论![]() 解得情况,
解得情况,![]() ,
,
当![]() 时,
时,
解得:![]() ,
,
即当![]() 时,不管
时,不管![]() 为何值时,
为何值时,![]() 无解,即
无解,即![]() 也无解;
也无解;
当![]() 时,方程
时,方程![]() 有两个根
有两个根![]() ,
,![]() ,假设
,假设![]() ,由于函数开口向上,故
,由于函数开口向上,故![]() 没有实数解,
没有实数解,
而![]()
函数的最小值为![]() ,故方程
,故方程![]() 的大根小于
的大根小于![]() ,即
,即![]()
故有 ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() 时,
时,![]() ,而
,而![]() 无解,满足条件,
无解,满足条件,
综上所述![]() 。
。


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】已知倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() :
:![]() 的焦点
的焦点![]() ,与抛物线
,与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过点![]() 的两条直线
的两条直线![]() 、
、![]() 分别交抛物线
分别交抛物线![]() 于点
于点![]() 、
、![]() 和
和![]() 、
、![]() ,线段
,线段![]() 和
和![]() 的中点分别为
的中点分别为![]() 、
、![]() .如果直线
.如果直线![]() 与
与![]() 的倾斜角互余,求证:直线
的倾斜角互余,求证:直线![]() 经过一定点.
经过一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一景区的截面图,![]() 是可以行走的斜坡,已知
是可以行走的斜坡,已知![]() 百米,
百米,![]() 是没有人行路(不能攀登)的斜坡,
是没有人行路(不能攀登)的斜坡,![]() 是斜坡上的一段陡峭的山崖.假设你(看做一点)在斜坡
是斜坡上的一段陡峭的山崖.假设你(看做一点)在斜坡![]() 上,身上只携带着量角器(可以测量以你为顶点的角).
上,身上只携带着量角器(可以测量以你为顶点的角).
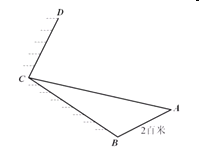
(1)请你设计一个通过测量角可以计算出斜坡![]() 的长的方案,用字母表示所测量的角,计算出
的长的方案,用字母表示所测量的角,计算出![]() 的长,并化简;
的长,并化简;
(2)设![]() 百米,
百米,![]() 百米,
百米,![]() ,
,![]() ,求山崖
,求山崖![]() 的长.(精确到米)
的长.(精确到米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,03,![]() ,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=3-x,g(x)=log3(x+8).
(1)求f(1),g(1),f[g(1)],g[f(1)]的值;
(2)求f[g(x)],g[f(x)]的表达式并说明定义域;
(3)说明f[g(x)],g[f(x)]的单调性(不需要证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com