
【题目】(选修4﹣5:不等式选讲)
已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)当a=﹣2时,求不等式f(x)<g(x)的解集;
(2)设a>﹣1,且当 ![]() 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
【答案】
(1)解:当a=﹣2时,求不等式f(x)<g(x)化为|2x﹣1|+|2x﹣2|﹣x﹣3<0.
设y=|2x﹣1|+|2x﹣2|﹣x﹣3,则 y=  ,它的图象如图所示:
,它的图象如图所示:
结合图象可得,y<0的解集为(0,2),故原不等式的解集为(0,2).
(2)解:设a>﹣1,且当 ![]() 时,f(x)=1+a,不等式化为 1+a≤x+3,故 x≥a﹣2对
时,f(x)=1+a,不等式化为 1+a≤x+3,故 x≥a﹣2对 ![]() 都成立.
都成立.
故﹣ ![]() ≥a﹣2,解得 a≤
≥a﹣2,解得 a≤ ![]() ,故a的取值范围为(﹣1,
,故a的取值范围为(﹣1, ![]() ].
].
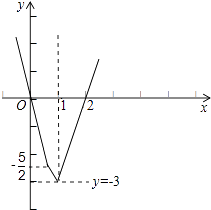
【解析】(1)当a=﹣2时,求不等式f(x)<g(x)化为|2x﹣1|+|2x﹣2|﹣x﹣3<0.设y=|2x﹣1|+|2x﹣2|﹣x﹣3,画出函数y的图象,数形结合可得结论.(2)不等式化即 1+a≤x+3,故 x≥a﹣2对 ![]() 都成立.故﹣
都成立.故﹣ ![]() ≥a﹣2,由此解得a的取值范围.
≥a﹣2,由此解得a的取值范围.
【考点精析】本题主要考查了函数单调性的性质和绝对值不等式的解法的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为θ= ![]() ,曲线C的参数方程为
,曲线C的参数方程为 ![]() .
.
(1)写出直线l与曲线C的直角坐标方程;
(2)过点M平行于直线l1的直线与曲线C交于A、B两点,若|MA||MB|= ![]() ,求点M轨迹的直角坐标方程.
,求点M轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
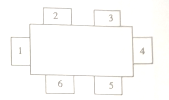
【题目】在一次体育兴趣小组的聚会中,要安排![]() 人的座位,使他们在如图所示的
人的座位,使他们在如图所示的![]() 个椅子中就坐,且相邻座位(如
个椅子中就坐,且相邻座位(如![]() 与
与![]() ,
, ![]() 与
与![]() )上的人要有共同的体育兴趣爱好.现已知这
)上的人要有共同的体育兴趣爱好.现已知这![]() 人的体育兴趣爱好如下表所示,且小林坐在
人的体育兴趣爱好如下表所示,且小林坐在![]() 号位置上,则
号位置上,则![]() 号位置上坐的是( )
号位置上坐的是( )

小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |
A. 小方 B. 小张 C. 小周 D. 小马
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC= ![]() .等边三角形ADB以AB为轴运动.
.等边三角形ADB以AB为轴运动. 
(1)当平面ADB⊥平面ABC时,求CD;
(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知二面角α﹣MN﹣β的大小为60°,菱形ABCD在面β内,A、B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O. 
(1)证明:AB⊥平面ODE;
(2)求异面直线BC与OD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 的椭圆
的椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
, ![]() 为椭圆上的任意一点,且
为椭圆上的任意一点,且![]() 成等差数列.
成等差数列.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆于
交椭圆于![]() 两点,若点
两点,若点![]() 始终在以
始终在以![]() 为直径的圆外,求实数
为直径的圆外,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com