
【题目】在锐角三角形![]() 中,若
中,若![]() ,则
,则![]() 的取值范围是__________.
的取值范围是__________.
【答案】![]()
【解析】由sinA=sin(π﹣A)=sin(B+C)=sinBcosC+cosBsinC,sinA=2sinBsinC,
可得sinBcosC+cosBsinC=2sinBsinC,①
由三角形ABC为锐角三角形,则cosB>0,cosC>0,
在①式两侧同时除以cosBcosC可得tanB+tanC=2tanBtanC,
又tanA=﹣tan(π﹣A)=﹣tan(B+C)=![]() ②,
②,
则tanAtanBtanC=﹣![]() tanBtanC,
tanBtanC,
由tanB+tanC=2tanBtanC可得tanAtanBtanC =![]() ,
,
令tanBtanC=t,由A,B,C为锐角可得tanA>0,tanB>0,tanC>0,
由②式得1﹣tanBtanC<0,解得t>1,
tanAtanBtanC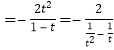 ,
,
由t>1得,﹣![]() ≤
≤![]() <0,
<0,
因此tanAtanBtanC的最小值为8,


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 
(1)当x≤0时,解不等式f(x)≥﹣1;
(2)写出该函数的单调区间;
(3)若函数g(x)=f(x)﹣m恰有3个不同零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:关于x的不等式x2+2ax+4>0对一切 ![]() 恒成立;q:函数f(x)=-(5-2a)x在R上是减函数.若“p或q”为真,“p且q”为假,求实数a的取值范围( )。
恒成立;q:函数f(x)=-(5-2a)x在R上是减函数.若“p或q”为真,“p且q”为假,求实数a的取值范围( )。
A.![]()
B.B、
C.C、
D.a≥-2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的方程2x2﹣ax﹣2=0的两根分别为α、β(α<β),函数![]()
(1)证明f(x)在区间(α,β)上是增函数;
(2)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列三个命题:
①若一个球的半径缩小到原来的 ![]() ,则其体积缩小到原来的
,则其体积缩小到原来的![]() ;
;
②若两组数据的平均数相等,则它们的标准差也相等;
③直线x+y+1=0与圆x2+y2= ![]() 相切.
相切.
其中真命题的序号是( )
A.①②③
B.①②
C.①③
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,在矩形ABCD中,
,在矩形ABCD中, ![]() ,
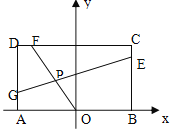
, ![]() ,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且![]() ,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com