
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到如表(单位:人):
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到如表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(Ⅰ)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(Ⅱ)①现从所抽取的30岁以上的网民中,按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人,然后,再从这10人中随机选出3人赠送优惠券,求选出的3人中至少有2人经常使用共享单车的概率.
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用共享单车的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: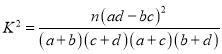 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(Ⅰ)能在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关;(Ⅱ)①
市使用共享单车情况与年龄有关;(Ⅱ)①![]() ;②
;②![]() ,
,![]()
【解析】
(Ⅰ)先根据公式计算卡方,再对照数据确定犯错误的概率,(Ⅱ)①先根据分层抽样确定人数,再根据古典概型概率公式求概率,②先确定随机变量服从二项分布,再根据二项分布得分布列与数学期望.
(Ⅰ)由列联表可知,![]() .
.
∵![]() ,
,
∴能在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关.
市使用共享单车情况与年龄有关.
(Ⅱ)①依题意,可知所抽取的10名30岁以上网民中,经常使用共享单车的有![]() (人),
(人),
偶尔或不用共享单车的有![]() (人).
(人).
则选出的3人中至少2人经常使用共享单车的概率为![]() .
.
②由![]() 列联表,可知抽到经常使用共享单位的频率为
列联表,可知抽到经常使用共享单位的频率为![]() ,
,
将频率视为概率,即从![]() 市市民中任意抽取1人,
市市民中任意抽取1人,
恰好抽到经常使用共享单车的市民的概率为![]() .
.
由题意得![]() ,∴
,∴![]() ;
;![]() .
.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,且
,且![]() ,
,![]() ,
,![]() 三点中恰有两点在抛物线
三点中恰有两点在抛物线![]() 上,另一点是抛物线
上,另一点是抛物线![]() 的焦点.
的焦点.
(1)求证:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)若直线![]() 过抛物线
过抛物线![]() 的焦点且与抛物线
的焦点且与抛物线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,点
,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为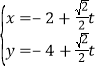 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,记直线
,记直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)求曲线![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)证明:![]() 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前共享单车基本覆盖饶城市区,根据统计,市区所有人骑行过共享单车的人数已占![]() ,骑行过共享单车的人数中,有
,骑行过共享单车的人数中,有![]() 是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
(1)任选出一名学生,求他(她)骑行过共享单车的概率;
(2)随着单车投放数量增加,乱停乱放成为城市管理的问题,如表是本市某组织累计投放单车数量![]() 与乱停乱放单车数量
与乱停乱放单车数量![]() 之间关系图表:
之间关系图表:
累计投放单车数量 | 100000 | 120000 | 150000 | 200000 | 230000 |
乱停乱放单车数量 | 1400 | 1700 | 2300 | 3000 | 3600 |
计算![]() 关于
关于![]() 的线性回归方程(其中
的线性回归方程(其中![]() 精确到
精确到![]() ,
,![]() 值保留三位有效数字),并预测当
值保留三位有效数字),并预测当![]() 时,单车乱停乱放的数量;
时,单车乱停乱放的数量;
(3)已知信州区、广丰区、上饶县、经开区四区中,其中有两个区的单车乱停乱放数量超过标准,在“大美上饶”活动中,检查组随机抽取两个区调查单车乱停乱放数量,![]() 表示“单车乱停乱放数量超过标准的区的个数”,求
表示“单车乱停乱放数量超过标准的区的个数”,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式和数据:回归直线方程![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
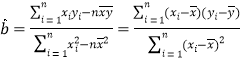 ,
,![]() ,
,
![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 分别是棱
分别是棱![]() 上的点,平面
上的点,平面![]() 平面
平面![]() .
.
(1)确定点![]() 的位置,并说明理由;
的位置,并说明理由;
(2)求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一布袋中装有![]() 个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
A. 若![]() ,则乙有必赢的策略B. 若
,则乙有必赢的策略B. 若![]() ,则甲有必赢的策略
,则甲有必赢的策略
C. 若![]() ,则甲有必赢的策略D. 若
,则甲有必赢的策略D. 若![]() ,则乙有必赢的策略
,则乙有必赢的策略
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点为极点,以
为参数),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若![]() 与曲线
与曲线![]() 相切,且
相切,且![]() 与坐标轴交于
与坐标轴交于![]() 两点,求以
两点,求以![]() 为直径的圆的极坐标方程.
为直径的圆的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋里装有![]() 个白球和
个白球和![]() 个红球,从口袋中任取
个红球,从口袋中任取![]() 个球.
个球.
(1)共有多少种不同的取法?
(2)其中恰有一个红球,共有多少种不同的取法?
(3)其中不含红球,共有多少种不同的取法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com