
【题目】已知数集![]() ,其中
,其中![]() ,且
,且![]() ,若对
,若对![]() ,
,![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() ,则称数集
,则称数集![]() 具有性质
具有性质![]() .
.
(1)分别判断数集![]() 与数集
与数集![]() 是否具有性质
是否具有性质![]() ,说明理由;
,说明理由;
(2)已知数集![]() 具有性质
具有性质![]() ,判断数列
,判断数列![]() ,
,![]() ,…,
,…,![]() 是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线E的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数).点P为曲线E上的动点,点Q为线段OP的中点.
(t为参数).点P为曲线E上的动点,点Q为线段OP的中点.
(1)求点Q的轨迹(曲线C)的直角坐标方程;
(2)若直线l交曲线C于A,B两点,点![]() 恰好为线段AB的三等分点,求直线l的普通方程.
恰好为线段AB的三等分点,求直线l的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),过线段
左侧),过线段![]() (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线![]() ,使得直线
,使得直线![]() 与抛物线
与抛物线![]() 在点
在点![]() 处的切线平行,设直线
处的切线平行,设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点.
两点.
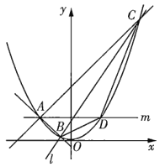
(1)记直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明:
,证明:![]() ;
;
(2)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年非洲爆发了埃博拉病毒疫情,在疫情结束后,当地防疫部门做了一项回访调查,得到如下结果,
患病 | 不患病 | |
有良好卫生习惯 | 20 | 180 |
无良好卫生习惯 | 80 | 220 |
(1)结合上面列联表,是否有![]() 的把握认为是否患病与卫生习惯有关?
的把握认为是否患病与卫生习惯有关?
(2)现从有良好卫生习惯且不患病的180人中抽取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共5人,再从这5人中选两人给市民做健康专题报告,求
共5人,再从这5人中选两人给市民做健康专题报告,求![]() ,
,![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
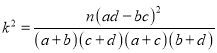
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=2sinx(sinx![]() cosx)﹣1图象向右平移
cosx)﹣1图象向右平移![]() 个单位得函数g(x)的图象,则下列命题中正确的是( )
个单位得函数g(x)的图象,则下列命题中正确的是( )
A.f(x)在(![]() ,
,![]() )上单调递增
)上单调递增
B.函数f(x)的图象关于直线x![]() 对称
对称
C.g(x)=2cos2x
D.函数g(x)的图象关于点(![]() ,0)对称
,0)对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com