
【题目】已知![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,满足
,满足![]() .
.
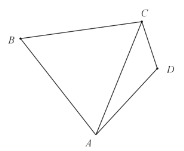
(1)求![]() 的大小;
的大小;
(2)如图,![]() ,在直线
,在直线![]() 的右侧取点
的右侧取点![]() ,使得
,使得![]() .当角
.当角![]() 为何值时,四边形
为何值时,四边形![]() 面积最大.
面积最大.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了美化环境,某公园欲将一块空地规划建成休闲草坪,休闲草坪的形状为如图所示的四边形ABCD.其中AB=3百米,AD=![]() 百米,且△BCD是以D为直角顶点的等腰直角三角形.拟修建两条小路AC,BD(路的宽度忽略不计),设∠BAD=
百米,且△BCD是以D为直角顶点的等腰直角三角形.拟修建两条小路AC,BD(路的宽度忽略不计),设∠BAD=![]() ,
,![]() (
(![]() ,
,![]() ).
).
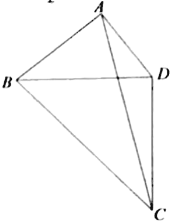
(1)当cos![]() =
=![]() 时,求小路AC的长度;
时,求小路AC的长度;
(2)当草坪ABCD的面积最大时,求此时小路BD的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当∠AOB为锐角时,求k的取值范围;
,当∠AOB为锐角时,求k的取值范围;
(3)若![]() ,
,![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点。
是否过定点。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级期末考试的学生中抽出 6![]() 名学生,其成绩(均为整数)的频率分布直方图如图所示.
名学生,其成绩(均为整数)的频率分布直方图如图所示.
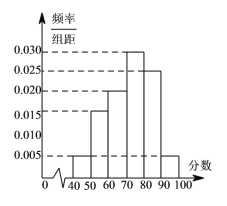
(1)估计这次考试的中位数
(2)假设分数在![]() 的学生的成绩都不相同,且都在
的学生的成绩都不相同,且都在![]() 分以上,现用简单随机抽样方法,从
分以上,现用简单随机抽样方法,从![]() 这
这 ![]() 个数中任取
个数中任取 ![]() 个数,求这
个数,求这 ![]() 个数恰好是两个学生的成绩的概率.
个数恰好是两个学生的成绩的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在长方体ABCD-A1B1C1D1中,AB=2,BC=2,CC1=3,长方体每条棱所在直线与过点C1的平面α所成的角都相等,则直线AC与平面α所成角的余弦值为( )
A. ![]() 或1 B.
或1 B. ![]() 或0 C.
或0 C. ![]() 或0 D.
或0 D. ![]() 或1
或1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个几何体的平面展开图,其中四边形ABCD为正方形,△PDC, △PBC, △PAB, △PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为 ( )

A. 平面BCD⊥平面PAD B. 直线BE与直线AF是异面直线
C. 直线BE与直线CF共面 D. 面PAD与面PBC的交线与BC平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com