
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
分析 利用三角恒等变换,化简函数f(x)的解析式,再利用正弦函数的周期性,求得实数w的值.
解答 解:由于函数f(x)=2sin2($\frac{w}{2}$x)+sin(wx-$\frac{π}{6}$)=2•$\frac{1-cos(wx)}{2}$)+sinwx•cos$\frac{π}{6}$-coswx•sin$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$sinwx-$\frac{3}{2}$cos(wx)+1
=$\sqrt{3}$sin(wx-$\frac{π}{3}$)+1(w>0),
∵f(x)的最小正周期为π,则 $\frac{2π}{w}$=π,∴实数w=2,
故选:D.
点评 本题主要考查三角恒等变换,正弦函数的周期性,属于基础题.


科目:高中数学 来源: 题型:选择题

| A. | ①⑤⑥,②③④ | B. | ①③⑤,②④⑥ | C. | ①②③,④⑤⑥ | D. | ①②⑥,③④⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
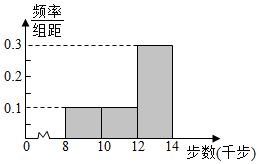 王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.
王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.| 每天的步数分组 (千步) | [8,10) | [10,12) | [12,14] |
| 评价级别 | 及格 | 良好 | 优秀 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
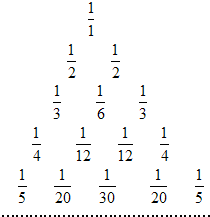 如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,
如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,| A. | $\frac{1}{2016×2015×2014}$ | B. | $\frac{1}{2016×2017}$ | C. | $\frac{1}{2016×2015×1006}$ | D. | $\frac{1}{2016×2015×1007}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是正方形,O是该正方形的中心,P是平面 ABCD 外一点,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是该正方形的中心,P是平面 ABCD 外一点,PO⊥底面ABCD,E是PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com