
【题目】已知二次函数![]() 的定义域为
的定义域为![]() 恰是不等式
恰是不等式![]() 的解集,其值域为
的解集,其值域为![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .
.
(1)求函数![]() 定义域为
定义域为![]() 和值域
和值域![]() ;
;
(2)是否存在负实数![]() ,使得
,使得![]() 成立?若存在,求负实数
成立?若存在,求负实数![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(3)若函数![]() 在定义域
在定义域![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了配合今年上海迪斯尼乐园工作,某单位设计了统计人数的数学模型![]() ,以
,以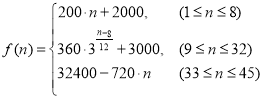 表示第
表示第![]() 个时刻进入园区的人数;以
个时刻进入园区的人数;以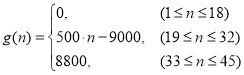 表示第
表示第![]() 个时刻离开园区的人数.设定以15分钟为一个计算单位,上午9点15分作为第1个计算人数单位,即
个时刻离开园区的人数.设定以15分钟为一个计算单位,上午9点15分作为第1个计算人数单位,即![]() ;9点30分作为第2个计算单位,即
;9点30分作为第2个计算单位,即![]() ;依次类推,把一天内从上午9点到晚上8点15分分成45个计算单位(最后结果四舍五入,精确到整数).
;依次类推,把一天内从上午9点到晚上8点15分分成45个计算单位(最后结果四舍五入,精确到整数).
(1)试计算当天14点至15点这1小时内进入园区的游客人数![]() 、离开园区的游客人数
、离开园区的游客人数![]()
![]() 各为多少?
各为多少?
(2)从13点45分(即![]() )开始,有游客离开园区,请你求出这之后的园区内游客总人数最多的时刻,并说明理由.
)开始,有游客离开园区,请你求出这之后的园区内游客总人数最多的时刻,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数![]() 图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
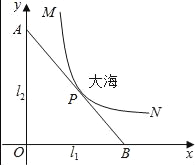
(1)求曲线段MPN的函数关系式,并指出其定义域;
(2)若某人从点O沿公路至点P观景,要使得沿折线OAP比沿折线OBP的路程更近,求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一研学实践活动小组利用课余时间,对某公司1月份至5月份销售某种产品的销售量及销售单价进行了调查,月销售单价![]() (单位:元)和月销售量
(单位:元)和月销售量![]() (单位:百件)之间的一组数据如下表所示:
(单位:百件)之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 |
月销售单价 | 1.6 | 1.8 | 2 | 2.2 | 2.4 |
月销售量 | 10 | 8 | 7 | 6 | 4 |
(1)根据1至5月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)预计在今后的销售中,月销售量与月销售单价仍然服从(1)中的关系,若该种产品的成本是1元/件,那么该产品的月销售单价应定为多少元才能获得最大月利润?(注:利润=销售收入-成本)
(回归直线方程![]() ,其中
,其中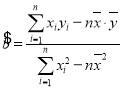 .参考数据:
.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的首项为p,公差为
的首项为p,公差为![]() ,对于不同的自然数
,对于不同的自然数![]() ,直线
,直线![]() 与
与![]() 轴和指数函数
轴和指数函数![]() 的图象分别交于点
的图象分别交于点![]() 与
与![]() (如图所示),记
(如图所示),记![]() 的坐标为
的坐标为![]() ,直角梯形
,直角梯形![]() 、
、![]() 的面积分别为
的面积分别为![]() 和
和![]() ,一般地记直角梯形
,一般地记直角梯形![]() 的面积为
的面积为![]() .
.

(1)求证:数列![]() 是公比绝对值小于1的等比数列;
是公比绝对值小于1的等比数列;
(2)设![]() 的公差
的公差![]() ,是否存在这样的正整数
,是否存在这样的正整数![]() ,构成以
,构成以![]() ,
,![]() ,
,![]() 为边长的三角形?并请说明理由;
为边长的三角形?并请说明理由;
(3)设![]() 的公差
的公差![]() 为已知常数,是否存在这样的实数p使得(1)中无穷等比数列
为已知常数,是否存在这样的实数p使得(1)中无穷等比数列![]() 各项的和
各项的和![]() ?并请说明理由.
?并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
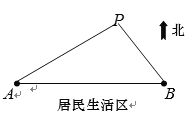
【题目】如图所示,![]() 、
、![]() 是两个垃圾中转站,
是两个垃圾中转站,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处,
千米处,![]() 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在
的南面为居民生活区.为了妥善处理生活垃圾,政府决定在![]() 的北面建一个垃圾发电厂
的北面建一个垃圾发电厂![]() .垃圾发电厂
.垃圾发电厂![]() 的选址拟满足以下两个要求(
的选址拟满足以下两个要求(![]() 、
、![]() 、
、![]() 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点
可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点![]() 到直线
到直线![]() 的距离要尽可能大).现估测得
的距离要尽可能大).现估测得![]() 、
、![]() 两个中转站每天集中的生活垃圾量分别约为
两个中转站每天集中的生活垃圾量分别约为![]() 吨和
吨和![]() 吨.设
吨.设![]() .
.
(1)求![]() (用
(用![]() 的表达式表示);
的表达式表示);
(2)垃圾发电厂该如何选址才能同时满足上述要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列六个命题:
(1)若![]() ,则函数
,则函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(2)![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(3)![]() 的反函数与
的反函数与![]() 是相同的函数.
是相同的函数.
(4)![]() 无最大值也无最小值.
无最大值也无最小值.
(5)![]() 的最小正周期为
的最小正周期为![]() .
.
(6)![]() 有对称轴两条,对称中心有三个.
有对称轴两条,对称中心有三个.
则正确命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com