练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．同样大小的正方体木块堆放在房间的一个角落里，如图所示，问这些木块中看不见的木块有多少个？

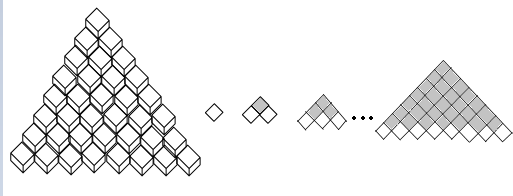
    分析 根据已知归纳可得堆放n层共有：1+（1+2）+（1+2+3）+…+（1+2+3+…+n）=$\frac{n（n+1）（n+2）}{6}$个正方体木块，进而得到答案．

    解答 解：由已知中正方体木块堆放方式可得：
    堆放1层共有：1个正方体木块；
    堆放2层共有：1+（1+2）个正方体木块；
    堆放3层共有：1+（1+2）+（1+2+3）个正方体木块；
    …
    归纳可得：堆放n层共有：1+（1+2）+（1+2+3）+…+（1+2+3+…+n）=$\frac{n（n+1）（n+2）}{6}$个正方体木块；
    由图可得：木块共堆放8层，故有$\frac{8×9×10}{6}$=120块．

    点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．已知命题p：“方程$\frac{{x}^{2}}{2m-1}$+$\frac{{y}^{2}}{2-m}$=m+2表示的曲线是椭圆”，命题q：“方程$\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{m-3}$=2m+1表示的曲线是双曲线”．且p∨q为真命题，p∧q为假命题，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．设二次函数f（x）=ax2+bx+1（a，b∈R，a＞0），方程f（x）=x的两个实数根为x1，x2，若0＜x1＜2，|x2-x1|=2，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若函数f（x）=x2-2x，则f（8）=48，f（x+1）=x2-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．抛物线y=$\frac{1}{4}$x2的焦点关于直线x-y-1=0的对称点的坐标是 （　　）
    A．（2，-1）B．（1，-1）C．（$\frac{1}{4}$，-$\frac{1}{4}$）D．（$\frac{1}{16}$，-$\frac{1}{16}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．命题：“?x∈R，x2+2ax+2-a=0”；命题q：已知函数f（x）=log2（a-2x）+x-2，f（x）存在零点，命题p∧q为真命题，求参数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．求函数y=$\frac{{x}^{4}+4{x}^{3}+17{x}^{2}+26x+106}{{x}^{2}+2x+7}$的最大值与最小值，其中|x|≤1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=$\frac{1}{\root{3}{{x}^{2}+2x+1}+\root{3}{{x}^{2}-1}+\root{3}{{x}^{2}-2x+1}}$，求f（1）+f（3）+f（5）+…+f（2k-1）+…+f（999）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知向量$\overrightarrow a=（3，1），\overrightarrow b=（1，3），\overrightarrow c=（k，2）$，若$（\overrightarrow a-\overrightarrow c）∥\overrightarrow b$，则k=$\frac{10}{3}$．

    查看答案和解析>>

    同步练习册答案