
分析 (1)①由题意列式求得2q10=1+q5,进一步得到$2{a}_{1}{q}^{m+10}={a}_{1}{q}^{m}+{a}_{1}{q}^{m+5}$,即bm+1,bm+11,bm+6(m∈N+}成等差数列;
②假设存在正整数k,使得(Sk)2,(Sk+10)2,(Sk+5)2成等差数列,由等差数列的性质可得${q}^{5}=-\frac{1}{2}$.代入S1,S13,S8验证不成立;
(2)由题意可得a1=1,a2=3,a3=5,b1=1,b2=2,b3=4,求得${a}_{n}=2n-1,{b}_{n}={2}^{n-1}$,结合s>1,t>1,可得从{an},{bn}中至少各取两项,然后分{bn}中不取1和{bn}中取1讨论求得:cn=n.
解答 (1)①证明:∵S3,S13,S8成等差数列,∴2S13=S3+S8,
又∵q≠1,∴$\frac{2{a}_{1}(1-{q}^{13})}{1-q}=\frac{{a}_{1}(1-{q}^{3})}{1-q}+\frac{{a}_{1}(1-{q}^{8})}{1-q}$,即2q13=q3+q8,
∴2q10=1+q5,则$2{a}_{1}{q}^{m+10}={a}_{1}{q}^{m}+{a}_{1}{q}^{m+5}$,即2bm+11=bm+1+bm+6,
∴bm+1,bm+11,bm+6成等差数列;
②解:假设存在正整数k,使得(Sk)2,(Sk+10)2,(Sk+5)2成等差数列,
则2(Sk+10)2=(Sk)2+(Sk+5)2,
∴$2(\frac{{a}_{1}(1-{q}^{k+10})}{1-q})^{2}=(\frac{{a}_{1}(1-{q}^{k})}{1-q})^{2}+(\frac{{a}_{1}(1-{q}^{k+5})}{1-q})^{2}$,
∴2(1-qk+10)2=(1-qk)2+(1-qk+5)2,
由2q10=1+q5,得${q}^{5}=-\frac{1}{2}$.
代入化简得:$\frac{9}{8}{q}^{2k}=0$.
∴q不存在;
(2)解:∵d>0,q>1.且{a1,a2,a3}∪{b1,b2,b3}={1,2,3,4,5},
∴a1=1,a2=3,a3=5,b1=1,b2=2,b3=4,
∴${a}_{n}=2n-1,{b}_{n}={2}^{n-1}$,
∵s>1,t>1,
∴从{an},{bn}中至少各取两项,
若{bn}中不取1,则{bn}中取出的数都是偶数,而数列{an}中全是奇数,
∴数列{Cn}中的项必是奇偶相间,
∵${b}_{n}={2}^{n}-1$,∴bn-bj<bk-bn,则取出的等比数列的项只能为两项,
数列{an}中的项最多取出三项,若取出的项多于三项,则数列{cn}中必有连续两项是数列{an}中的项,
∴(s+t)max=5,
另外,要使得(s+t)max=5,数列{cn}不可能是bi,aj,bm,an,bk,…,
∵bm-bi<bk-bm,∴{cn}不可能是等差数列.
下面证明(s+t)max=5能取到:
设数列{cn}的公差为d1,
∵ai,bj,am,bn,ak成等差数列,
∴${d}_{1}={2}^{j-1}-(2i-1)$,
∴bk=ai+3d1,即2k-1=3•2j-1-2(2i-1)且h≥j+1,
若h≥j+2,则2k-1≥2j+1,即3•2j-1-2(2i-1)≥2j+1,
化简得:-2(2i-1)≥2j-1,矛盾,
∴h=j+1,
∴3•2j-1-2(2i-1)=2j,有2i-1=2j-2,
∵2i-1为奇数,∴j=2,h=3.
∴bj=b2=2,bk=b3=4,
∴cn=n;
若数列{bn}中取1,可以将1看成数列{an},
则数列{cn}为1,bi,aj,bm,an,
∴bm=1+3d1,即2m-1=1+3(2i-1-1),
若m≥i+2,则2m-1≥2i+1,即3•2i-1-2≥2i+1,
化简得:-2≥2i-1,矛盾.
∴m=i+1,
∴22=3•2i-1-2,即2i-1=2,得i=2,
∴bi=b2=2,
∴cn=n.
综上所得:cn=n.
点评 本题考查数列递推式,考查了数列的函数特性,考查了等差数列的性质,训练了学生的逻辑思维能力和运算求解能力,属难题.


科目:高中数学 来源: 题型:选择题
 如图是甲、乙两组各5名同学体重(单位:kg)数据的茎叶图.设甲、乙两组数据的平均数依次为$\overline{{x}_{1}}$和$\overrightarrow{{x}_{2}}$,方差依次为s${\;}_{1}^{2}$和s${\;}_{3}^{2}$,那么( )
如图是甲、乙两组各5名同学体重(单位:kg)数据的茎叶图.设甲、乙两组数据的平均数依次为$\overline{{x}_{1}}$和$\overrightarrow{{x}_{2}}$,方差依次为s${\;}_{1}^{2}$和s${\;}_{3}^{2}$,那么( )| A. | $\overline{{x}_{1}}>\overline{{x}_{2}}$,${s}_{1}^{2}{>s}_{2}^{2}$ | B. | $\overline{{x}_{1}}>\overline{{x}_{2}}$,${s}_{1}^{2}{<s}_{2}^{2}$ | ||
| C. | $\overline{{x}_{1}}<\overline{{x}_{2}}$,${s}_{1}^{2}{<s}_{2}^{2}$ | D. | $\overline{{x}_{1}}<\overline{{x}_{2}}$,${s}_{1}^{2}{>s}_{2}^{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
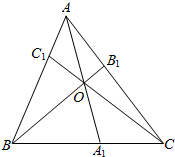 如图,已知点O是△ABC内任意一点,连结AO,BO,CO,并延长交对边于A1,B1,C1,则$\frac{{O{A_1}}}{{A{A_1}}}+\frac{{O{B_1}}}{{B{B_1}}}+\frac{{O{C_1}}}{{C{C_1}}}=1$,类比猜想:点O是空间四面体V-BCD内的任意一点,连结VO,BO,CO,DO并延长分别交面BCD,VCD,VBD,VBC于点V1,B1,C1,D1,则有$\frac{{O{V_1}}}{{V{V_1}}}+\frac{{O{B_1}}}{{B{B_1}}}+\frac{{O{C_1}}}{{C{C_1}}}+\frac{{O{D_1}}}{{D{D_1}}}=1$.
如图,已知点O是△ABC内任意一点,连结AO,BO,CO,并延长交对边于A1,B1,C1,则$\frac{{O{A_1}}}{{A{A_1}}}+\frac{{O{B_1}}}{{B{B_1}}}+\frac{{O{C_1}}}{{C{C_1}}}=1$,类比猜想:点O是空间四面体V-BCD内的任意一点,连结VO,BO,CO,DO并延长分别交面BCD,VCD,VBD,VBC于点V1,B1,C1,D1,则有$\frac{{O{V_1}}}{{V{V_1}}}+\frac{{O{B_1}}}{{B{B_1}}}+\frac{{O{C_1}}}{{C{C_1}}}+\frac{{O{D_1}}}{{D{D_1}}}=1$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 一质点的移动方式,如图所示,在第1分钟,它从原点移动到点(1,0),接下来它便依图上所示的方向,在x,y轴的正向前进或后退,每1分钟只走1单位且平行其中一轴,则2016分钟结束之时,质点的位置坐标是(44,8).
一质点的移动方式,如图所示,在第1分钟,它从原点移动到点(1,0),接下来它便依图上所示的方向,在x,y轴的正向前进或后退,每1分钟只走1单位且平行其中一轴,则2016分钟结束之时,质点的位置坐标是(44,8).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | {0} | C. | {x|x∈R,x≠0} | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com