
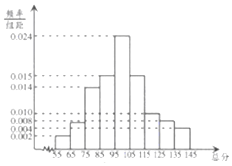
 从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.
从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.分析 (1)一组中的数据用该组区间的中点值作代表,求这100份数学试卷的样本平均分$\overline x$和样本方差s2;
(2)①利用该正态分布,Z~N(100,366),即可求P(81<z<119);
②数学总分位于区间(81,119)的概率为0.6826,X~(2400,0.6826),即可求EX.
解答 解:(1)由题意,$\overline{x}$=60×0.02+70×0.08+80×0.14+90×0.15+100×0.24+110×0.15+120×0.1+130×0.08+140×0.04=100,
样本方差s2=(60-100)2×0.02+(70-100)2×0.08+(80-100)2×0.14+(90-100)2×0.15+(100-100)2×0.24+(110-100)2×0.15+(120-100)2×0.1+(130-100)2×0.08+(140-100)2×0.04=366;
(2)Z~N(100,366),P(81<z<119)=P(100-19<z<100+19)=0.6826;
②数学总分位于区间(81,119)的概率为0.6826,X~(2400,0.6826),
EX=2400×0.6826=1638.24.
点评 本题考查频率分布直方图的应用,样本方差的求法,正态分布,考查分析问题解决问题的能力,属于中档题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
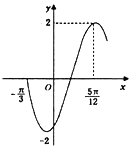 函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.
函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(2k-\frac{1}{4},2k+\frac{1}{4}),k∈Z$ | B. | $(2k+\frac{1}{2},2k+\frac{5}{2}),k∈Z$ | ||
| C. | $(4k-\frac{1}{4},4k+\frac{1}{4}),k∈Z$ | D. | $(4k+\frac{1}{4},4k+\frac{15}{4}),k∈Z$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (-∞,0) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
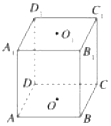 如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.
如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com