
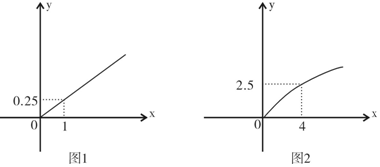
分析 (1)根据函数的模型设出函数解析式,从两个图中分别找出特殊点坐标,代入函数解析式求出两个函数解析式.
(2)将企业获利表示成对产品B投资x的函数;将函数中的$\sqrt{10-x}$换元为t,将函数转化为二次函数,求出对称轴,求出函数的最值.
解答 解:(1)设y=k1x,由0.25=k1x1得:k1=0.25
设y=k2$\sqrt{x}$,由2.5=k2$\sqrt{4}$得k2=1.25
∴所求函数为y=0.25x及y=1.25$\sqrt{x}$…(4分)
(2)设投入A产品x万元,则投入B产品为10-x万元,企业获得的利润为y=0.25x+1.25$\sqrt{10-x}$…(6分)
令$\sqrt{10-x}$=t(0≤t≤10)则
y=$\frac{1}{4}$(10-t2)+$\frac{5}{4}$t=$\frac{1}{4}$(-t2+5t+10)
=$\frac{1}{4}$[-(t-$\frac{5}{2}$)2+$\frac{65}{4}$]…(8分)
当t=$\frac{5}{2}$时,y取得最大值$\frac{65}{16}$万元,此时x=3.75万元
故对A、B两种产品分别投资3.75万元、6.25万元时,企业可获得最大利润$\frac{65}{16}$万元.…(10分)
点评 本题考查将实际问题的最值问题转化为函数的最值问题、考查利用待定系数法求函数的解析式、考查换元法注意新变量的范围、二次函数的最值与对称轴有关.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2-b2>1 | B. | a2-b2≥1 | C. | a2-b2<1 | D. | a2-b2≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com