
| 1 |
| 3 |
| 3 |
| 8 |
| 1 |
| cos2x |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 9 |
| a+b+c |
| 1 |
| cos2α |
| 1 |
| cos2β |
| 1 |
| cos2γ |
| 9 |
| cos2α+cos2β+cos2γ |
| 1 |
| 3 |
| 1 |
| cos2x |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 9 |
| a+b+c |
| 1 |
| cos2α |
| 1 |
| cos2β |
| 1 |
| cos2γ |
| 9 |
| cos2α+cos2β+cos2γ |
| 9 |
| cos2α+cos2β+cos2γ |
| 9 |
| 3-(sin2α+sin2β+sin2γ) |
| 9 | ||
3-
|
| 27 |
| 8 |
| 27 |
| 8 |
| 3 |
| 8 |


科目:高中数学 来源: 题型:
 (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市毕业班(第二轮)质量检测理科数学试卷(解析版) 题型:解答题
如图,四棱柱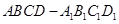 中,
中,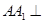 平面
平面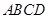 .
.

(Ⅰ)从下列①②③三个条件中选择一个做为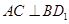 的充分条件,并给予证明;
的充分条件,并给予证明;
①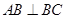 ,②
,②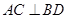 ;③
;③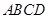 是平行四边形.
是平行四边形.
(Ⅱ)设四棱柱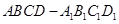 的所有棱长都为1,且
的所有棱长都为1,且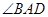 为锐角,求平面
为锐角,求平面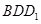 与平面
与平面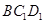 所成锐二面角
所成锐二面角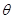 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013年福建省泉州市高三5月质检数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com