
【题目】已知f(x)=3x+m3﹣x为奇函数.
(1)求函数g(x)=f(x)﹣ ![]() 的零点;
的零点;
(2)若对任意t∈R的都有f(t2+a2﹣a)+f(1+2at)≥0恒成立,求实数a的取值范围.
【答案】
(1)解:∵f(x)是奇函数,∴f(0)=0,
解得:m=﹣1,
∴f(x)=3x﹣3﹣x,令g(x)=0,即3x﹣3﹣x﹣ ![]() =0,
=0,
令t=3x,则t﹣ ![]() ﹣
﹣ ![]() =0,
=0,
即3t2﹣8t﹣3=0,解得:t=3或t=﹣ ![]() ,
,
∵t=3x≥0,∴t=3即x=1,
∴函数g(x)的零点是1;
(2)解:∵对任意t∈R的都有f(t2+a2﹣a)+f(1+2at)≥0恒成立,
∴f(t2+a2﹣a)≥﹣f(1+2at)对任意t∈R恒成立,
∵f(x)在R是奇函数也是增函数,
∴f(t2+a2﹣a)≥﹣f(﹣1﹣2at)对任意t∈R恒成立,
即t2+a2﹣a≥﹣1﹣2at对任意t∈R恒成立,
即t2+2at+a2﹣a+1≥0对任意t∈R恒成立,
∴△=(2a)2﹣4(a2﹣a+1)≤0,
∴a≤1,实数a的范围是(﹣∞,1].
【解析】(1)根据函数的奇偶性得到f(0)=0,求出m的值,从而求出f(x)的解析式,令g(x)=0,求出函数的零点即可;(2)根据函数的奇偶性和单调性,问题转化为t2+2at+a2﹣a+1≥0对任意t∈R恒成立,根据二次函数的性质求出a的范围即可.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知射线OA:x﹣y=0(x≥0),OB:2x+y=0(x≥0).过点P(1,0)作直线分别交射线OA,OB于点A,B.
(1)当AB的中点在直线x﹣2y=0上时,求直线AB的方程;
(2)当△AOB的面积取最小值时,求直线AB的方程.
(3)当PAPB取最小值时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1且loga3>loga2,若函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为1.
(1)求a的值;
(2)解不等式 ![]() ;
;
(3)求函数g(x)=|logax﹣1|的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示. (Ⅰ)计算第三组的样本数;并估计该校高一年级1000名学生中身高在170厘米以下的人数;
(Ⅱ)估计被随机抽取的这100名学生身高的中位数、平均数.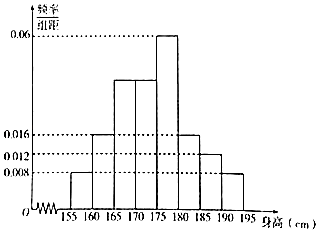
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴交于点D,且有|FA|=|FD|,当点A的横坐标为3时,△ADF为正三角形
(1)求C的方程
(2)延长AF交抛物线于点E,过点E作抛物线的切线l1 , 求证:l1∥l.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知△ABC的顶点A(5,1),B(1,5).
(1)若A为直角△ABC的直角顶点,且顶点C在y轴上,求BC边所在直线方程;
(2)若等腰△ABC的底边为BC,且C为直线l:y=2x+3上一点,求点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 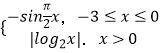 ,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+
,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+ ![]() 的取值范围为( )
的取值范围为( )
A.(﹣1,+∞)
B.(﹣1,1)
C.(﹣∞,1)
D.[﹣1,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体ABCD中,AB=CD=2 ![]() ,AD=BD=3,AC=BC=4,点E,F,G,H分别在棱AD,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是 .
,AD=BD=3,AC=BC=4,点E,F,G,H分别在棱AD,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com