
【题目】给定下列函数:①f(x)= ![]() ②f(x)=﹣|x|③f(x)=﹣2x﹣1 ④f(x)=(x﹣1)2 , 满足“对任意x1 , x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的条件是( )
②f(x)=﹣|x|③f(x)=﹣2x﹣1 ④f(x)=(x﹣1)2 , 满足“对任意x1 , x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的条件是( )
A.①②③
B.②③④
C.①②④
D.①③④
【答案】A
【解析】解:因为对任意x1 , x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2),故满足条件的函数是一个减函数.
对于①,函数是反比例函数,其在(0,+∞)是一个减函数,满足题意;
对于②,f(x)=﹣|x|,其在(0,+∞)是一个减函数,满足题意;
对于③,函数是一次函数,其在(0,+∞)是一个减函数,满足题意;
对于④,函数f(x)=(x﹣1)2在(0,1)是减函数,在(1,+∞)上是增函数,故不满足题意;
故选A.
【考点精析】解答此题的关键在于理解函数的单调性的相关知识,掌握注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种,以及对函数奇偶性的性质的理解,了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】为迎接2017年“双![]() ”,“双
”,“双![]() ”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共
”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共![]() 个,生产一个汤碗需
个,生产一个汤碗需![]() 分钟,生产一个花瓶需
分钟,生产一个花瓶需![]() 分钟,生产一个茶杯需
分钟,生产一个茶杯需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时.若生产一个汤碗可获利润
小时.若生产一个汤碗可获利润![]() 元,生产一个花瓶可获利润
元,生产一个花瓶可获利润![]() 元,生产一个茶杯可获利润
元,生产一个茶杯可获利润![]() 元.
元.
(1)使用每天生产的汤碗个数![]() 与花瓶个数
与花瓶个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过![]() 关者奖励
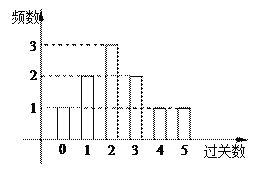
关者奖励![]() 件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
(Ⅰ)求小明在这十次游戏中所得奖品数的均值;
(Ⅱ)规定过三关者才能玩另一个高级别的游戏,估计小明一次游戏后能玩另一个游戏的概率;
(Ⅲ)已知小明在某四次游戏中所过关数为{2,2,3,4},小聪在某四次游戏中所过关数为{3,3,4,5},现从中各选一次游戏,求小明和小聪所得奖品总数超过10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() //
// ![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() , 点
, 点![]() 是
是![]() 边的中点, 将△
边的中点, 将△![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() , 得到如图所示的几何体.
, 得到如图所示的几何体.
(Ⅰ)求证: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,求二面角
,求二面角![]() 的大小.
的大小.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面结论正确的是( )
①一个数列的前三项是1,2,3,那么这个数列的通项公式![]() .
.
②由平面三角形的性质推测空间四面体的性质,这是一种合理推理.
③在类比时,平面中的三角形与空间中的平行六面体作为类比对象较为合适.
④“所有3的倍数都是9的倍数,某数![]() 一定是9的倍数,则
一定是9的倍数,则![]() 一定是9的倍数”,这是三段论推理,但其结论是错误的.
一定是9的倍数”,这是三段论推理,但其结论是错误的.
A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 为参数)上的每一点的横坐标保持不变,纵坐标变为原来的
为参数)上的每一点的横坐标保持不变,纵坐标变为原来的![]() 倍,得到曲线
倍,得到曲线![]()
(1)求出![]() 的普通方程;
的普通方程;
(2)设直线![]() :
: ![]() 与
与![]() 的交点为
的交点为![]() ,
, ![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,求过线段
轴正半轴为极轴建立极坐标系,求过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com