
����Ŀ��ij���ֽ�Ŀ����ѡ�ֳַ�����ѵ������������ѡ�Σ���50λ��ѡ�ֵij����ɼ����ܷ�150�֣��ֳ�[90��100����[100��110����[110��120����[120��130����[130��140��5�����ͳ�ƣ��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
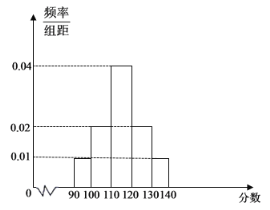
��1������Ƶ�ʷ���ֱ��ͼ��������50��ѡ�ֳ����ɼ���ƽ���֣���������涨�ɼ����ڻ����120�ֵ�ѡ�ֿɻ�ý�Ŀ����֯����ѵ�ʸ�120�����£�������120��������̭������50�����л����ѵ�ʸ��������
��2����Ŀ��ӻ����ѵ�ʸ����Ա��ѡ�β�����Ա���븴��.Ϊ���ӽ�Ŀ�������ԣ���Ŀ���ṩ���������ֽ��븴���ķ�ʽ��ÿλѡ��ֻ��ѡ������һ�֣�
��һ�ַ�ʽ�����÷ֲ�����ķ�����ȡ6��ѡ�ֲμӸ�����
�ڶ��ַ�ʽ��ÿ�������5�δ�����ᣬ�ۼƴ��3�����3����ֹ���⣬���3��ɲμӸ���
����֪�ij����ɼ���[120��130���ڣ������ÿһ������ĸ���Ϊ![]() �����һ���֮��û��Ӱ���Ҫ��μӸ�����ѡ�����ַ�ʽ��������
�����һ���֮��û��Ӱ���Ҫ��μӸ�����ѡ�����ַ�ʽ��������
������ѡ��ڶ��ַ�ʽ�������ڴ�������д������X�ķֲ��к���ѧ����.
���𰸡���1��115��15��2����ѡ��ڶ��ַ�ʽ���������������
��������
��1��ÿ����е���Ϊ����ֵ��Ȩƽ�����ɵõ�ƽ����������Ƶ�ʷֲ�ֱ��ͼ���Ƴ������ɼ����ڻ����120�ֵĸ��ʣ����ɵõ���50�����л����ѵ�ʸ��������
��2���ٷֱ����ײ������ַ�ʽ�����ܽ��븴���ĸ��ʣ����ʴ�ĸ�������
���г��������![]() �����п��ܵ�ȡֵ���ֱ�����Ӧ���ʣ��г��ֲ������������ɣ�
�����п��ܵ�ȡֵ���ֱ�����Ӧ���ʣ��г��ֲ������������ɣ�
��1��ƽ���ɼ�![]() ��95��0.01+105��0.02+115��0.04+125��0.02+135��0.01����10��115��
��95��0.01+105��0.02+115��0.04+125��0.02+135��0.01����10��115��
���л����ѵ�ʸ������Ϊ��0.02+0.01����10��50��15.
��2��������ͼ��֪���ɼ�������120�ֵ�ѡ�ֵ������ֱ�Ϊ10�ˣ�5�ˣ�
�������ܲμ���ѵ��Ϊ�¼�A��
���ײ��õ�һ�ַ�ʽ��
���÷ֲ�����ķ�����ȡ6����Ա���ڵ�4�飬��5���зֱ��ȡ4�ˣ�2�ˣ�
��P��A��![]() ����ѡ��ѡ��ڶ��鷽ʽ������Ϊ�״�Ե�һ����ĸ���Ϊp
����ѡ��ѡ��ڶ��鷽ʽ������Ϊ�״�Ե�һ����ĸ���Ϊp![]() ��
��
�����Լ״���3���Ҵ�Եĸ���Ϊp3![]() .
.
�״���4����ǡ��3�δ�Եĸ���Ϊ![]() ��
��
�״���5����ǡ��3�δ�Եĸ���Ϊ![]() ��
��
�ɴ˿ɵ�P��A��![]() ��
��
��![]() ��
��
�����μӸ���ѡ��ڶ��ַ�ʽ������.
�ڼ״��ÿһ��ĸ���Ϊp![]() ���������X�Ŀ���ȡֵΪ3��4��5��
���������X�Ŀ���ȡֵΪ3��4��5��
��P��X��3����p3+��1��p��3![]() ��
��
P��X��4��![]() ��
��
P��X��5��![]() ��
��
��X�ķֲ���Ϊ��
X | 3 | 4 | 5 |
P |
|
|
|
��X����ѧ����E��X����3![]() 4
4![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijij��ѧ����רҵ400��ѧ���μ�ij�β�����������Ůѧ������������ʹ�÷ֲ�����ķ������������ȡ��100��ѧ������¼���ǵķ����������ݷֳ�7�飺 ![]() ���������õ�����Ƶ�ʷֲ�ֱ��ͼ��
���������õ�����Ƶ�ʷֲ�ֱ��ͼ��
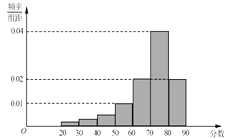
���������400��ѧ���������ȡһ�ˣ����������С��70�ĸ��ʣ�
������֪�����з���С��40��ѧ����5�ˣ��Թ��������з���������[40,50���ڵ�������
������֪��������һ�������ķ�����С��70���������з�����С��70����Ů��������ȣ��Թ���������������Ů�������ı�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�·����˼ס������ֲ�ͬ�ͺŵ��ֻ�����˾ͳ���������߶��������ͺ��ֻ�������������������µ��״�ͼ��������˵������ȷ���ǣ� ��
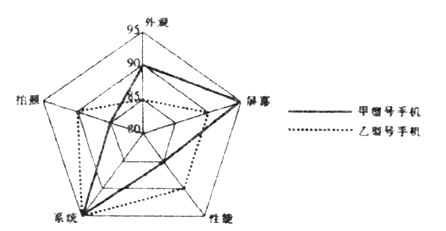
A. ���ͺ��ֻ�����۷���ȽϺ�.B. �ס������ͺŵ�ϵͳ������ͬ.
C. ���ͺ��ֻ������ܷ���ȽϺ�.D. ���ͺ��ֻ������շ���ȽϺ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
�� ![]() �ֱ�Ϊ˫����
�ֱ�Ϊ˫����![]() �����ҽ��㣬
�����ҽ��㣬 ![]() Ϊ˫���ߵ��㣬��
Ϊ˫���ߵ��㣬��![]() ��
�� ![]() Ϊֱ����Բ��˫����ij����������
Ϊֱ����Բ��˫����ij����������![]() ��
�� ![]() ���㣬������
���㣬������![]() �����˫���ߵ�������Ϊ________.
�����˫���ߵ�������Ϊ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ԲC��![]() 1��a��b��0����������Ϊ
1��a��b��0����������Ϊ![]() �����᳤Ϊ2��ֱ��l��ԲO��x2+y2
�����᳤Ϊ2��ֱ��l��ԲO��x2+y2![]() ���У�������ԲC�ཻ��M��N����.
���У�������ԲC�ཻ��M��N����.
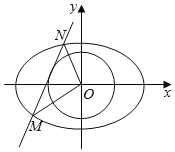
��1������ԲC�ķ��̣�
��2��֤����![]()
![]() Ϊ��ֵ.
Ϊ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��ǰn���Ϊ
��ǰn���Ϊ![]() ��������
��������![]() �ĸ�����¹������У�
�ĸ�����¹������У�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ��������������ͽ��ۣ���
��������������ͽ��ۣ���![]() ��������
��������![]() ��
��![]() ��
��![]() ��
��![]() �����ǵȱ����У�������
�����ǵȱ����У�������![]() ��
��![]() ��
��![]() ��
��![]() ������ǰ
������ǰ![]() ���Ϊ
���Ϊ![]() ����������������
����������������![]() ��ʹ
��ʹ![]() ��
��![]() ����
����![]() .������ȷ�Ľ�����_____.��������Ϊ��ȷ�Ľ�����Ŷ����ϣ�
.������ȷ�Ľ�����_____.��������Ϊ��ȷ�Ľ�����Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������۹��ɶ����Ĺ����У��������������ṩ������������������![]() ���ȵ�.������������Ϊ���������������ڴ˻����Ͻ�һ���о����õ����¹��ɣ������������е�ijһ����
���ȵ�.������������Ϊ���������������ڴ˻����Ͻ�һ���о����õ����¹��ɣ������������е�ijһ����![]() ��ȷ��������������1��������ƽ���������ڵ�������������ô��������������������һ�鹴�����������������е�ijһ����
��ȷ��������������1��������ƽ���������ڵ�������������ô��������������������һ�鹴�����������������е�ijһ����![]() �Ǵ���2��ż������������2����ƽ����Ȼ������ƽ�����ֱ��1����1���õ����������������ż������һ�鹴����.�ɴ˵õ������ֹ�������֮Ϊ����
�Ǵ���2��ż������������2����ƽ����Ȼ������ƽ�����ֱ��1����1���õ����������������ż������һ�鹴����.�ɴ˵õ������ֹ�������֮Ϊ����![]() ���ɵ�һ�鹴������.������17���ɵ����鹴�������ġ�������Ϊ
���ɵ�һ�鹴������.������17���ɵ����鹴�������ġ�������Ϊ![]() ������20���ɵ����鹴�������ġ�������Ϊ
������20���ɵ����鹴�������ġ�������Ϊ![]() ����
����![]() ____________.
____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC��,��A,B,C�ĶԱ߷ֱ�Ϊa,b,c,��B��A,C�ĵȲ�����.
��1����![]() ,���c��ֵ;
,���c��ֵ;
��2����t=sinAsinC,��t��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com