
【题目】如图,已知圆![]() 与
与![]() 轴的左右交点分别为
轴的左右交点分别为![]() ,与
,与![]() 轴正半轴的交点为
轴正半轴的交点为![]() .
.
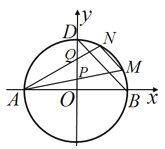
(1)若直线![]() 过点
过点![]() 并且与圆
并且与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若点![]() 是圆
是圆![]() 上第一象限内的点,直线
上第一象限内的点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是线段
是线段![]() 的中点,直线
的中点,直线![]() ,求直线
,求直线![]() 的斜率.
的斜率.
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
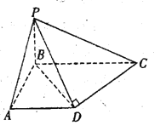
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,异面直线
,异面直线![]() 和
和![]() 所成角等于
所成角等于![]() .
.
(1)求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ?若存在,指出点
?若存在,指出点![]() 在棱
在棱![]() 上的位置;若不存在,说明理由.
上的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是一个容量为20的样本数据分组后的频率分布表:
分组 |
|
|
|
| ||
频数 | 4 | 2 | 6 | 8 | ||
(1)请估计样本的平均数;
(2)以频率估计概率,若样本的容量为2000,求在分组![]() 中的频数;
中的频数;
(3)若从数据在分组![]() 与分组
与分组![]() 的样本中随机抽取2个,求恰有1个样本落在分组
的样本中随机抽取2个,求恰有1个样本落在分组![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 的图象大致为( )
的图象大致为( )
A.  B.
B. 
C.  D.
D. 
【答案】C
【解析】
由函数的解析式 ,当![]() 时,是函数的一个零点,属于排除A,B,
时,是函数的一个零点,属于排除A,B,
当x∈(0,1)时,cosx>0,![]() ,函数f(x) <0,函数的图象在x轴下方,排除D.
,函数f(x) <0,函数的图象在x轴下方,排除D.
本题选择C选项.
点睛:函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.
【题型】单选题
【结束】
12
【题目】设![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com