
【题目】给定方程: ![]() ,则下列命题中:
,则下列命题中:
①该方程没有小于0的实数解;
②该方程有无数个实数解;
③该方程在(-∞,0)内有且只有一个实数解;
④若x0是该方程的实数解,则x0>-1.
正确的命题是________.
【答案】②③④
【解析】试题分析:根据正弦函数的符号和指数函数的性质,可得该方程存在小于0的实数解,故①不正确;根据指数函数的图象与正弦函数的有界性,可得方程有无数个正数解,故②正确;根据y=(![]() )x﹣1的单调性与正弦函数的有界性,
)x﹣1的单调性与正弦函数的有界性,
分析可得当x≤﹣1时方程没有实数解,当﹣1<x<0时方程有唯一实数解,由此可得③④都正确.
解:对于①,若α是方程(![]() )x+sinx﹣1=0的一个解,
)x+sinx﹣1=0的一个解,
则满足(![]() )α=1﹣sinα,当α为第三、四象限角时(
)α=1﹣sinα,当α为第三、四象限角时(![]() )α>1,
)α>1,
此时α<0,因此该方程存在小于0的实数解,得①不正确;
对于②,原方程等价于(![]() )x﹣1=﹣sinx,
)x﹣1=﹣sinx,
当x≥0时,﹣1<(![]() )x﹣1≤0,而函数y=﹣sinx的最小值为﹣1
)x﹣1≤0,而函数y=﹣sinx的最小值为﹣1
且用无穷多个x满足﹣sinx=﹣1,
因此函数y=(![]() )x﹣1与y=﹣sinx的图象在[0,+∞)上有无穷多个交点
)x﹣1与y=﹣sinx的图象在[0,+∞)上有无穷多个交点
因此方程(![]() )x+sinx﹣1=0有无数个实数解,故②正确;
)x+sinx﹣1=0有无数个实数解,故②正确;
对于③,当x<0时,
由于x≤﹣1时(![]() )x﹣1≥1,函数y=(
)x﹣1≥1,函数y=(![]() )x﹣1与y=﹣sinx的图象不可能有交点
)x﹣1与y=﹣sinx的图象不可能有交点
当﹣1<x<0时,存在唯一的x满足(![]() )x=1﹣sinx,
)x=1﹣sinx,
因此该方程在(﹣∞,0)内有且只有一个实数解,得③正确;
对于④,由上面的分析知,
当x≤﹣1时(![]() )x﹣1≥1,而﹣sinx≤1且x=﹣1不是方程的解
)x﹣1≥1,而﹣sinx≤1且x=﹣1不是方程的解
∴函数y=(![]() )x﹣1与y=﹣sinx的图象在(﹣∞,﹣1]上不可能有交点
)x﹣1与y=﹣sinx的图象在(﹣∞,﹣1]上不可能有交点
因此只要x0是该方程的实数解,则x0>﹣1.
故答案为:②③④


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某高校学生社团为了解“大数据时代”下大学生就业情况的满意度,对20名学生进行问卷计分调查(满分100分),得到如图所示的茎叶图:
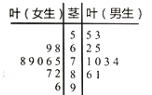
(1)计算男生打分的平均分,观察茎叶图,评价男女生打分的分散程度;
(2)从打分在80分以上的同学随机抽3人,求被抽到的女生人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:直线y=(2m+1)x+m﹣2的图象不经过第四象限,q:方程x2+ ![]() =1表示焦点在x轴上的椭圆,若(¬p)∨q为假命题,求实数m的取值范围.
=1表示焦点在x轴上的椭圆,若(¬p)∨q为假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在某商业区周边有 两条公路![]() 和
和![]() ,在点
,在点![]() 处交汇,该商业区为圆心角
处交汇,该商业区为圆心角![]() ,半径3
,半径3![]() 的扇形,现规划在该商业区外修建一条公路
的扇形,现规划在该商业区外修建一条公路![]() ,与
,与![]() ,
,![]() 分别交于
分别交于![]() ,要求
,要求![]() 与扇形弧相切,切点
与扇形弧相切,切点![]() 不在
不在![]() ,
,![]() 上.
上.
(1)设![]() 试用
试用![]() 表示新建公路
表示新建公路![]() 的长度,求出
的长度,求出![]() 满足的关系式,并写出
满足的关系式,并写出![]() 的范围;
的范围;
(2)设![]() ,试用
,试用![]() 表示新建公路
表示新建公路![]() 的长度,并且确定
的长度,并且确定![]() 的位置,使得新建公路
的位置,使得新建公路![]() 的长度最短.
的长度最短.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,圆
,圆![]() 的圆心
的圆心![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 到椭圆
到椭圆![]() 的右焦点的距离为
的右焦点的距离为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,且
,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点, 直线
两点, 直线![]() 交圆
交圆![]() 于
于![]() 两点, 且
两点, 且![]() 为
为![]() 的中点, 求
的中点, 求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直线坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为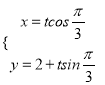 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的参数方程;
的参数方程;
(2)设点![]() 在
在![]() 上,
上, ![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +
+ ![]() 的两个极值点分别为x1 , x2 , 且x1∈(0,1),x2∈(1,+∞);点P(m,n)表示的平面区域为D,若函数y=loga(x+4)(a>1)的图象上存在区域D内的点,则实数a的取值范围是( )
的两个极值点分别为x1 , x2 , 且x1∈(0,1),x2∈(1,+∞);点P(m,n)表示的平面区域为D,若函数y=loga(x+4)(a>1)的图象上存在区域D内的点,则实数a的取值范围是( )
A.(1,3]
B.(1,3)
C.(3,+∞)
D.[3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的图象与g(x)=logax(a>0,且a≠1)的图象关于x轴对称,且g(x)的图象过(4,2)点.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若f(x﹣1)>f(5﹣x),求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com