
已知函数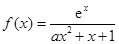 ,其中
,其中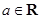 .
.
(1)若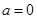 ,求函数
,求函数 的定义域和极值;
的定义域和极值;
(2)当 时,试确定函数
时,试确定函数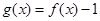 的零点个数,并证明.
的零点个数,并证明.
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
设f(x)是(-∞,+∞)上的奇函数,f(x+2)=-f(x),当0≤x≤1时,f(x)=x.
(1)求f(π)的值;
(2)当-4≤x≤4时,求f(x)的图象与x轴所围图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,把边长为10的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设其高为h,体积为V(不计接缝).
(1)求出体积V与高h的函数关系式并指出其定义域;
(2)问当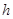 为多少时,体积V最大?最大值是多少?
为多少时,体积V最大?最大值是多少?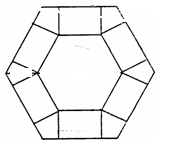
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 a为常数且a>0.
a为常数且a>0.
(1)证明:函数f(x)的图像关于直线x= 对称;
对称;
(2)若x0满足f(f(x0))= x0,但f(x0)≠x0,则x0称为函数f(x)的二阶周期点,如果f(x)有两个二阶周期点x1,x2,试确定a的取值范围;
(3)对于(2)中的x1,x2,和a,设x3为函数f(f(x))的最大值点,A(x1,f(f(x1))),B(x2,f(f(x2))),C(x3,0),记△ABC的面积为S(a),讨论S(a)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
函数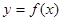 的定义域为
的定义域为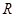 ,若存在常数
,若存在常数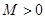 ,使得
,使得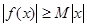 对一切实数
对一切实数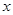 均成立,则称
均成立,则称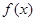 为“圆锥托底型”函数.
为“圆锥托底型”函数.
(1)判断函数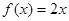 ,
,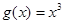 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.
(2)若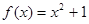 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出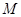 的最大值.
的最大值.
(3)问实数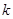 、
、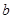 满足什么条件,
满足什么条件,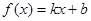 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com