
【题目】已知函数![]() 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意![]() ,恒有
,恒有![]() ;②对于定义域上的任意
;②对于定义域上的任意![]() ,
, ![]() ,当
,当![]() 时,恒有
时,恒有![]() ,则称函数
,则称函数![]() 为“理想函数”.在下列三个函数中:(1)
为“理想函数”.在下列三个函数中:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .“理想函数”有__________.(只填序号)
.“理想函数”有__________.(只填序号)
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润![]() 与时间
与时间![]() 的关系,可选用( )
的关系,可选用( )
A. 一次函数 B. 二次函数 C. 指数型函数 D. 对数型函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】社会调查人员希望从对人群的随机抽样调查中得到对他们所提问题诚实的回答,但是被采访者常常不愿意如实做出应答.
1965年Stanley·L.Warner发明了一种应用概率知识来消除这种不愿意情绪的方法.Warner的随机化应答方法要求人们随机地回答所提问题中的一个,而不必告诉采访者回答的是哪个问题,两个问题中有一个是敏感的或者是令人为难的,另一个是无关紧要的,这样应答者将乐意如实地回答问题,因为只有他知道自己回答的是哪个问题.
假如在调查运动员服用兴奋剂情况的时候,无关紧要的问题是:你的身份证号码的尾数是奇数吗;敏感的问题是:你服用过兴奋剂吗.然后要求被调查的运动员掷一枚硬币,如果出现正面,就回答第一个问题,否则回答第二个问题.
例如我们把这个方法用于200个被调查的运动员,得到56个“是”的回答,请你估计这群运动员中大约有百分之几的人服用过兴奋剂.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
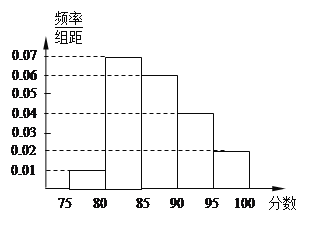
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A、B、C所对的边分别是a、b、c,向量m=(cos B,cos C),n=(2a+c,b),且m⊥n.
(1)求角B的大小;
(2)若b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图像与函数h(x)=![]() 的图像关于点A(0,1)对称。
的图像关于点A(0,1)对称。
(1)求函数f(x)的解析式;
(2)若g(x)=xf(x)+ax,且g(x)在区间(0,4]上为减函数,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注: 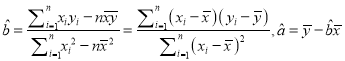 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com