
【题目】为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,整理如下:
甲公司员工![]() :410,390,330,360,320,400,330,340,370,350
:410,390,330,360,320,400,330,340,370,350
乙公司员工![]() :360,420,370,360,420,340,440,370,360,420
:360,420,370,360,420,340,440,370,360,420
每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件0.65元,乙公司规定每天350件以内(含350件)的部分每件0.6元,超出350件的部分每件0.9元.
(1)根据题中数据写出甲公司员工![]() 在这10天投递的快件个数的平均数和众数;
在这10天投递的快件个数的平均数和众数;
(2)为了解乙公司员工![]() 每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为
每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)根据题中数据估算两公司被抽取员工在该月所得的劳务费.
【答案】(1)平均数为360,众数为330;(2)见详解;(3)甲公司:7020(元),乙公司:7281(元)
【解析】
(1)将图中甲公司员工A的所有数据相加,再除以总的天数10,即可求出甲公司员工A投递快递件数的平均数.从中发现330出现的次数最多,故为众数;
(2)由题意能求出![]() 的可能取值为340,360,370,420,440,分别求出相对应的概率,由此能求出
的可能取值为340,360,370,420,440,分别求出相对应的概率,由此能求出![]() 的分布列和数学期望;
的分布列和数学期望;
(3)利用(1)(2)的结果,可估算两公司的每位员工在该月所得的劳务费.
解:(1)由题意知
甲公司员工![]() 在这10天投递的快递件数的平均数为
在这10天投递的快递件数的平均数为
![]() .
.
众数为330.
(2)设乙公司员工![]() 1天的投递件数为随机变量
1天的投递件数为随机变量![]() ,则
,则
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
![]() 的分布列为
的分布列为
| 204 | 219 | 228 | 273 | 291 |
|
|
|
|
|
|
![]() (元);
(元);
(3)由(1)估计甲公司被抽取员工在该月所得的劳务费为
![]() (元)
(元)
由(2)估计乙公司被抽取员工在该月所得的劳务费为
![]() (元).
(元).


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知数列{![]() }的首项a1=2,前n项和为
}的首项a1=2,前n项和为![]() ,且数列{
,且数列{![]() }是以
}是以![]() 为公差的等差数列·
为公差的等差数列·
(1)求数列{![]() }的通项公式;
}的通项公式;
(2)设![]() ,
,![]() ,数列{
,数列{![]() }的前n项和为
}的前n项和为![]() ,
,
①求证:数列{![]() }为等比数列,
}为等比数列,
②若存在整数m,n(m>n>1),使得![]() ,其中
,其中![]() 为常数,且
为常数,且![]() -2,求
-2,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击运动员在比赛前进行三周的封闭训练,教练员将其每天成绩的均值数据整理,并绘成条形图如下,
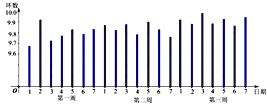
根据该图,下列说法错误的是:( )
A.第三周平均成绩最好B.第一周平均成绩比第二平均成绩好
C.第一周成绩波动较大D.第三周成绩比较稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前n项
的前n项![]() ,
,![]() ,…,
,…,![]() 的最大项为
的最大项为![]() ,第n项之后的各项
,第n项之后的各项![]() ,
,![]() ,…的最小项为
,…的最小项为![]() ,
,![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,写出
,写出![]() ,
,![]() ,
,![]() ;
;
(2)若数列![]() 的通项公式为
的通项公式为![]() ,判断
,判断![]() 是否为等差数列,若是,求出公差;若不是,请说明理由;
是否为等差数列,若是,求出公差;若不是,请说明理由;
(3)若数列![]() 为公差大于零的等差数列,求证:
为公差大于零的等差数列,求证:![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).
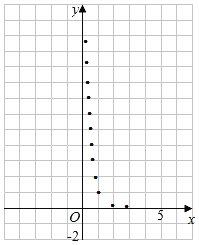

表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间y关于开关旋钮旋转的弧度数x的回归方程类型?(不必说明理由)
哪一个更适宜作烧水时间y关于开关旋钮旋转的弧度数x的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立y关于x的回归方程;
(3)若旋转的弧度数x与单位时间内煤气输出量t成正比,那么x为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为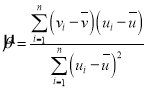 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com