
分析 求出$\overrightarrow{OA},\overrightarrow{OB}$的夹角,建立平面直角坐标系,设出$\overrightarrow{OA},\overrightarrow{OB}$的坐标,判断C的轨迹.
解答 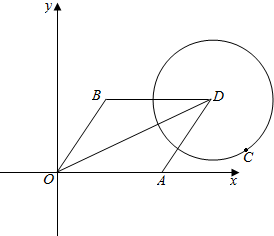 解:∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=1,∴$\sqrt{2}×\sqrt{2}$×cos<$\overrightarrow{OA},\overrightarrow{OB}$>=1,∴cos<$\overrightarrow{OA},\overrightarrow{OB}$>=$\frac{1}{2}$.
解:∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=1,∴$\sqrt{2}×\sqrt{2}$×cos<$\overrightarrow{OA},\overrightarrow{OB}$>=1,∴cos<$\overrightarrow{OA},\overrightarrow{OB}$>=$\frac{1}{2}$.
∴$\overrightarrow{OA},\overrightarrow{OB}$的夹角为$\frac{π}{3}$.
设$\overrightarrow{OA}=(\sqrt{2},0)$,$\overrightarrow{OB}$=($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{6}}{2}$),设$\overrightarrow{OA}+\overrightarrow{OB}$=$\overrightarrow{OD}$.则$\overrightarrow{OD}$=$\overrightarrow{OA}+\overrightarrow{OB}$=($\frac{3\sqrt{2}}{2}$,$\frac{\sqrt{6}}{2}$),
∴|$\overrightarrow{OD}$|=$\sqrt{6}$,∵|$\overrightarrow{OA}$+$\overrightarrow{CB}$|=1,∴|$\overrightarrow{OA}$+$\overrightarrow{OB}$-$\overrightarrow{OC}$|=1,即|$\overrightarrow{OD}$-$\overrightarrow{OC}$|=|$\overrightarrow{CD}$|=1.
∴C在以D为圆心,以1为半径的圆上,
∴|$\overrightarrow{OC}$|的最小值为$\sqrt{6}-1$,|$\overrightarrow{OC}$|的最大值是$\sqrt{6}$+1.
故答案为[$\sqrt{6}$-1,$\sqrt{6}$+1].
点评 本题考查了平面向量的数量积运算,建立平面直角坐标系,判断C点轨迹是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
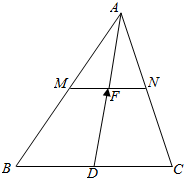 在△ABC中,已知A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于点F,求$\overrightarrow{DF}$的坐标.
在△ABC中,已知A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于点F,求$\overrightarrow{DF}$的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com