
【题目】定义在(0,+∞)上的函数f(x)=a(x+ ![]() )﹣|x﹣
)﹣|x﹣ ![]() |(a∈R).
|(a∈R).
(1)当a= ![]() 时,求f(x)的单调区间;
时,求f(x)的单调区间;
(2)若f(x)≥ ![]() x对任意的x>0恒成立,求a的取值范围.
x对任意的x>0恒成立,求a的取值范围.
【答案】
(1)解:当a= ![]() 时,f(x)=
时,f(x)= 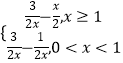 ,
,
当x≥1时,f(x)= ![]() ﹣
﹣ ![]() 的导数为f′(x)=﹣
的导数为f′(x)=﹣ ![]() ﹣
﹣ ![]() <0;
<0;
当0<x<1时,f(x)= ![]() ﹣
﹣ ![]() 的导数为f′(x)=
的导数为f′(x)= ![]() +
+ ![]() >0;
>0;
所以f(x)的单调递增区间是(0,1],单调递减区间是[1,+∞).
(2)解:由f(x)≥ ![]() x得a(x+
x得a(x+ ![]() )﹣|x﹣
)﹣|x﹣ ![]() |≥
|≥ ![]() x,x>0,
x,x>0,
可得a(x2+1)﹣|x2﹣1|≥ ![]() x2,
x2,
①当0<x<1时,a(x2+1)+(x2﹣1)≥ ![]() x2,
x2,
即有a≥ ![]() ,
,
由 ![]() =
= ![]() ﹣
﹣ ![]() ∈(
∈( ![]() ,1)
,1)
可得a≥1;
②当x≥1时,a(x2+1)﹣(x2﹣1)≥ ![]() x2,
x2,
可得a≥ ![]()
由 ![]() =
= ![]() ﹣
﹣ ![]() ∈[
∈[ ![]() ,
, ![]() )
)
可得a≥ ![]() .
.
综上所述,a的取值范围是[ ![]() ,+∞).
,+∞).
【解析】(1)求出a= ![]() 时,讨论当x≥1时,当0<x<1时,去掉绝对值,求得导数,判断符号,即可得到所求单调区间;(2)由f(x)≥
时,讨论当x≥1时,当0<x<1时,去掉绝对值,求得导数,判断符号,即可得到所求单调区间;(2)由f(x)≥ ![]() x可得a(x2+1)﹣|x2﹣1|≥
x可得a(x2+1)﹣|x2﹣1|≥ ![]() x2 , 讨论当0<x<1时,当x≥1时,运用参数分离和函数的单调性可得最值,进而得到a的范围.
x2 , 讨论当0<x<1时,当x≥1时,运用参数分离和函数的单调性可得最值,进而得到a的范围.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列各题中p是q的什么条件.
(1)p:|x|=|y|,q:x=y;
(2)p:△ABC是直角三角形,q:△ABC是等腰三角形;
(3)p:四边形的对角线互相平分,q:四边形是矩形;
(4)p:圆x2+y2=r2(r>0)与直线ax+by+c=0相切,q:c2=(a2+b2)r2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知
中,已知![]()
![]() 平面
平面![]() ,且四边形
,且四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.

(I)求证: ![]()
![]() 平面
平面![]() ;
;
(Ⅱ)点![]() 是线段
是线段![]() 上的动点,当直线
上的动点,当直线![]() 与
与![]() 所成角最小时,求线段
所成角最小时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1 , F2 , P为双曲线上一点,且
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , P为双曲线上一点,且 ![]()
![]() =0,△F1PF2的内切圆半径r=2a,则双曲线的离心率e= .
=0,△F1PF2的内切圆半径r=2a,则双曲线的离心率e= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 为等比数列,
为等比数列,![]() ,公比为
,公比为![]() ,且
,且![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)若![]() ,求
,求![]() ;
;
(2)若调换![]() 的顺序后能构成一个等差数列,求
的顺序后能构成一个等差数列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常数![]() ,使得对任意正整数
,使得对任意正整数![]() ,不等式
,不等式![]() 总成立?若存在,求出
总成立?若存在,求出![]() 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a是从集合{1,2,3,4}中随机取出的一个数,b是从集合{1,2,3}中随机取出的一个数,构成一个基本事件(a,b)。记“在这些基本事件中,满足logba≥1为事件A,则A发生的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列4个命题,其中正确命题的个数是( )
①计算:9192除以100的余数是1;
②命题“x>0,x﹣lnx>0”的否定是“x>0,x﹣lnx≤0”;
③y=tanax(a>0)在其定义域内是单调函数而且又是奇函数;
④命题p:“|a|+|b|≤1”是命题q:“对任意的x∈R,不等式asinx+bcosx≤1恒成立”的充分不必要条件.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com