
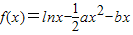 .
.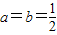 时,求f(x)的最大值;
时,求f(x)的最大值;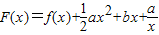 ,(0<x≤3),其图象上任意一点P(x,y)处切线的斜率k≤
,(0<x≤3),其图象上任意一点P(x,y)处切线的斜率k≤ 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;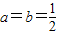 代入函数解析式,求其导数,根据求解目标,这个导数在函数定义域内只有一个等于零的点,判断这唯一的极值点是极大值点即可;
代入函数解析式,求其导数,根据求解目标,这个导数在函数定义域内只有一个等于零的点,判断这唯一的极值点是极大值点即可; 恒成立,分离参数后转化为函数的最值;
恒成立,分离参数后转化为函数的最值;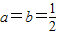 时,
时, ,
,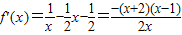 (2′)
(2′)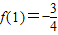 ,此即为最大值…(4分)
,此即为最大值…(4分)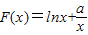 ,x∈(0,3],则有
,x∈(0,3],则有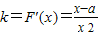 ≤
≤ ,在x∈(0,3]上恒成立,
,在x∈(0,3]上恒成立,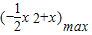 ,x∈(0,3],
,x∈(0,3],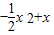 取得最大值
取得最大值 ,
, …(8分)
…(8分)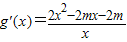 .
.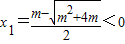 (舍去),
(舍去),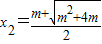 ,
,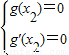 既
既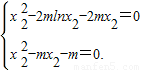
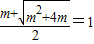 ,解得
,解得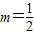 .…(12分)
.…(12分)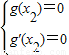 ,由这个方程组求解m使用了构造函数通过函数的性质得到x2的方法也是值得仔细体会的技巧.
,由这个方程组求解m使用了构造函数通过函数的性质得到x2的方法也是值得仔细体会的技巧. 

 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
(07年宁夏、 海南卷理)(12分)
设函数![]()
(I)若当![]() 时,
时,![]() 取得极值,求
取得极值,求![]() 的值,并讨论
的值,并讨论![]() 的单调性;
的单调性;
(II)若![]() 存在极值,求
存在极值,求![]() 的取值范围,并证明所有极值之和大于
的取值范围,并证明所有极值之和大于![]() .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省高三(奥班)10月月考理科数学试卷(解析版) 题型:解答题
选修4-5:不等式选讲(本小题满分10分)
设函数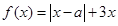 ,其中
,其中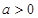 。
。
(Ⅰ)当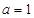 时,求不等式
时,求不等式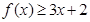 的解集;
的解集;
(Ⅱ)若不等式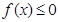 的解集为
的解集为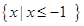 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年新人教版高三一轮复习单元测试(8)数学试卷 题型:解答题
(12分)(理)设函数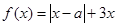 ,其中
,其中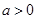 。
。
(Ⅰ)当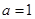 时,求不等式
时,求不等式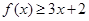 的解集;
的解集;
(Ⅱ)若不等式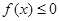 的解集为
的解集为 ,求a的值。
,求a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com