
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求数列
,求数列![]() 前
前![]() 项和
项和![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)当![]() 时,
时, ![]()
![]() 两式相减可得,验
两式相减可得,验![]() 可得
可得![]() 是以首项为2,公比为2等比数列,进而可得结果;(Ⅱ)结合(Ⅰ)可得
是以首项为2,公比为2等比数列,进而可得结果;(Ⅱ)结合(Ⅰ)可得![]() 利用错位相减法求和可得结果.
利用错位相减法求和可得结果.
试题解析:(Ⅰ) ![]()
当![]() 时,
时, ![]() 则
则![]() ,
,
当![]() 时,
时, ![]()
![]()
两式相减,得![]() 所以
所以![]()
所以![]() 是以首项为2,公比为2等比数列,
是以首项为2,公比为2等比数列,
所以![]()
(Ⅱ)因为![]()
![]()
![]()
两式相减,得即
![]()
![]()
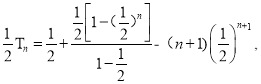
![]() 所以
所以![]()
【易错点晴】本题主要考查数列的通项及等比数列、“错位相减法”求数列的和,属于难题. “错位相减法”求数列的和是重点也是难点,利用“错位相减法”求数列的和应注意以下几点:①掌握运用“错位相减法”求数列的和的条件(一个等差数列与一个等比数列的积);②相减时注意最后一项 的符号;③求和时注意项数别出错;④最后结果一定不能忘记等式两边同时除以![]() .
.


科目:高中数学 来源: 题型:
【题目】有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=![]() , AD=1,DC⊥BC,则这块菜地的面积为
, AD=1,DC⊥BC,则这块菜地的面积为 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下图中,四边形 ABCD是等腰梯形, ![]() ,
, ![]() ,O、Q分别为线段AB、CD的中点,OQ与EF的交点为P,OP=1,PQ=2,现将梯形ABCD沿EF折起,使得
,O、Q分别为线段AB、CD的中点,OQ与EF的交点为P,OP=1,PQ=2,现将梯形ABCD沿EF折起,使得![]() ,连结AD、BC,得一几何体如图所示.
,连结AD、BC,得一几何体如图所示.
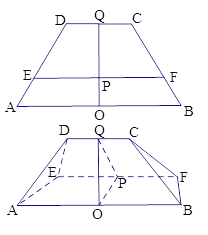
(Ⅰ)证明:平面ABCD![]() 平面ABFE;
平面ABFE;
(Ⅱ)若上图中, ![]() ,CD=2,求平面ADE与平面BCF所成锐二面角的余弦值.
,CD=2,求平面ADE与平面BCF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4x﹣2x+1+3,当x∈[﹣2,1]时,f(x)的最大值为m,最小值为n,
(1)若角α的终边经过点P(m,n),求sinα+cosα的值;
(2)g(x)=mcos(nx+![]() )+n,求g(x)的最大值及自变量x的取值集合.
)+n,求g(x)的最大值及自变量x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)在(﹣∞,0)上单调递减,且f(2)=0,则不等式xf(x﹣1)>0的解集是( )
A.(﹣3,﹣1)
B.(﹣3,1)∪(2,+∞)
C.(﹣3,0)∪(3,+∞)
D.(﹣1,0)∪(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且(2b-c)cos A=acos C.
(1)求角A的大小;
(2)若a=3,b=2c,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com