
【题目】已知等比数列{an}、等差数列{bn},满足a1>0,b1=a1﹣1,b2=a2 , b3=a3且数列{an}唯一.
(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和.
【答案】解:(1)设等比数列{an}的公比为q,
∵b1=a1﹣1,b2=a2 , b3=a3 , 且{bn}为等差数列,
∴2a2=(a1﹣1)+a3 ,
即2a1q=(a1﹣1)+a1q2 ,
即(q﹣1)2=![]() ,
,
∵数列{an}唯一,
∴q在{q|q≠0}上只有一个解,
∴(q﹣1)2=![]() 中有一个解为q=0,
中有一个解为q=0,
故![]() =1,此时,a1=1,q=2;
=1,此时,a1=1,q=2;
故数列{an}是以1为首项,2为公比的等比数列,
数列{bn}是以0为首项,2为公差的等差数列;
故an=2n﹣1 , bn=2n﹣2;
(2)anbn=(2n﹣2)2n﹣1 ,
Sn=01+22+4×4+6×8+…+(2n﹣2)2n﹣1 ,
2Sn=02+24+4×8+6×16+…+(2n﹣2)2n ,
两式作差可得,
Sn=﹣2×2+(﹣2)×4+(﹣2)×8+…+(﹣2)×2n﹣1+(2n﹣2)2n
=(2n﹣2)2n﹣(22+23+24+…+2n)
=(n﹣1)2n+1﹣![]()
=(n﹣2)2n+1+4.
【解析】(1)设等比数列{an}的公比为q,从而可得(q﹣1)2=![]() , 从而结合数列{an}唯一可得a1=1,q=2;从而解得.
, 从而结合数列{an}唯一可得a1=1,q=2;从而解得.
(2)化简anbn=(2n﹣2)2n﹣1 , 结合通项公式的形式可知利用错位相减法求其前n项和。
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系 即可以解答此题.
即可以解答此题.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】已知F1是椭圆5x2+9y2=45的左焦点,P为椭圆上半部分任意一点,A(1,1)为椭圆内一点,则|PA|+|PF1|的最小值_______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 , 其中a∈R.若对任意的非零实数x1 , 存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则k的取值范围为( )
, 其中a∈R.若对任意的非零实数x1 , 存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则k的取值范围为( )
A.k≤0
B.k≥8
C.0≤k≤8
D.k≤0或k≥8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如图.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm.
(Ⅰ)检查人员从这15条鱼中,随机抽出3条,求3条中恰有1条汞含量超标的概率;
(Ⅱ)若从这批数量很大的鱼中任选3条鱼,记ξ表示抽到的汞含量超标的鱼的条数.以此15条鱼的样本数据来估计这批数量很大的鱼的总体数据,求ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F是抛物线y2=4x的焦点,点A,B在该抛物线上且位于x轴的两侧,OA⊥OB(其中O为坐标原点),则△AOB与△AOF面积之和的最小值是( )
A.16
B.8![]()
C.8![]()
D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx(sinx+![]() cosx).
cosx).
(1)求f(x)的最小正周期和最大值;
(2)在锐角三角形ABC中,角A,B,C的对边分别为a,b,c,若f(![]() )=1,a=2
)=1,a=2![]() , 求三角形ABC面积的最大值.
, 求三角形ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.
(I)用t表示出PQ的长度,并探求△CPQ的周长l是否为定值;
(Ⅱ)设探照灯照射在正方形ABCD内部区域的面积S(平方百米),求S的最大值.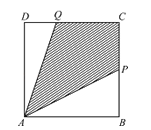
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com