
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)对该快递点近![]() 天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为
天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,那么从这
件,那么从这![]() 天中随机抽出
天中随机抽出![]() 天,求这
天,求这![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件的概率.
件的概率.
【答案】(1)![]() 一个包裹,
一个包裹,![]() 一个包裹时花费的运费最少,为
一个包裹时花费的运费最少,为![]() 元;(2)
元;(2)![]() .
.
【解析】
(1)分![]() 一个包裹,
一个包裹,![]() 一个包裹,
一个包裹,![]() 一个包裹,
一个包裹,![]() 一个包裹,
一个包裹,![]() 一个包裹,
一个包裹,![]() 一个包裹三种情况讨论;
一个包裹三种情况讨论;
(2)采用枚举法,枚举出基本事件总数以及事件“![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件”所包含的基本事件个数,再利用古典概型的概率计算公式计算即可.
件”所包含的基本事件个数,再利用古典概型的概率计算公式计算即可.
解:![]() 一个包裹,
一个包裹,![]() 一个包裹时,需花费
一个包裹时,需花费![]() (元),
(元),
![]() 一个包裹,
一个包裹,![]() 一个包裹时,需花费
一个包裹时,需花费![]() (元),
(元),
![]() 一个包裹,
一个包裹,![]() 一个包裹时,需花费
一个包裹时,需花费![]() (元),
(元),
综上,![]() 一个包裹,
一个包裹,![]() 一个包裹时花费的运费最少,为
一个包裹时花费的运费最少,为![]() 元.
元.
![]() 天中有
天中有![]() 天的日揽包裹数超过
天的日揽包裹数超过![]() 件,
件,
记这三天为![]() 其余两天为
其余两天为![]()
从![]() 天中随机抽出
天中随机抽出![]() 天的所有基本事件如下:
天的所有基本事件如下:
![]() ,
,![]() ,
,![]()
一共![]() 种,
种,
![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件的基本事件有,
件的基本事件有,![]() 一共
一共![]() 种,
种,
所以从这![]() 天中随机抽出
天中随机抽出![]() 天,
天,
![]() 天的日揽件数均超过
天的日揽件数均超过![]() 件的概率为
件的概率为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,四边形ABCD为平行四边形,BD⊥DC,△PCD为正三角形,平面PCD⊥平面ABCD,E为PC的中点.
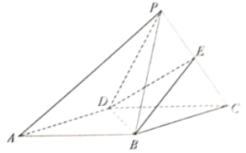
(1)证明:AP∥平面EBD;
(2)证明:BE⊥PC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 有共同的焦点,且离心率为
有共同的焦点,且离心率为![]() ,设
,设![]() 分别是
分别是![]() 为椭圆的上下顶点
为椭圆的上下顶点
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 与
与![]() 轴不垂直的直线
轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,当弦
,当弦![]() 的中点
的中点![]() 落在四边形
落在四边形![]() 内(含边界)时,求直线
内(含边界)时,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点P(4,0)的动直线与抛物线C:![]() 交于点A,B,且
交于点A,B,且![]() (点O为坐标原点).
(点O为坐标原点).
(1)求抛物线C的方程;
(2)当直线AB变动时,x轴上是否存在点Q使得点P到直线AQ,BQ的距离相等,若存在,求出点Q坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人2018年的家庭总收人为![]() 元,各种用途占比如图中的折线图,
元,各种用途占比如图中的折线图,![]() 年家庭总收入的各种用途占比统计如图中的条形图,已知
年家庭总收入的各种用途占比统计如图中的条形图,已知![]() 年的就医费用比
年的就医费用比![]() 年的就医费用增加了
年的就医费用增加了![]() 元,则该人
元,则该人![]() 年的储畜费用为( )
年的储畜费用为( )

A.![]() 元B.
元B.![]() 元C.
元C.![]() 元D.
元D.![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台![]() 的轴截面为等腰梯形
的轴截面为等腰梯形![]() ,
,![]() 圆台
圆台![]() 的侧面积为
的侧面积为![]() .若点
.若点![]() 分别为圆
分别为圆![]() 上的动点,且点
上的动点,且点![]() 在平面
在平面![]() 的同侧.
的同侧.

(1)求证:![]() ;
;
(2)若![]() ,则当三棱锥
,则当三棱锥![]() 的体积取最大值时,求
的体积取最大值时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆Q经过定点![]() ,且与定直线
,且与定直线![]() 相切(其中a为常数,且
相切(其中a为常数,且![]() ).记动圆圆心Q的轨迹为曲线C.
).记动圆圆心Q的轨迹为曲线C.
(1)求C的方程,并说明C是什么曲线?
(2)设点P的坐标为![]() ,过点P作曲线C的切线,切点为A,若过点P的直线m与曲线C交于M,N两点,则是否存在直线m,使得
,过点P作曲线C的切线,切点为A,若过点P的直线m与曲线C交于M,N两点,则是否存在直线m,使得![]() ?若存在,求出直线m斜率的取值范围;若不存在,请说明理由.
?若存在,求出直线m斜率的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com