
【题目】关于![]() 的方程
的方程![]() ,给出下列四个判断:
,给出下列四个判断:
①存在实数![]() ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
②存在实数![]() ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
③存在实数![]() ,使得方程恰有6个不同的实根;
,使得方程恰有6个不同的实根;
④存在实数![]() ,使得方程恰有8个不同的实根;
,使得方程恰有8个不同的实根;
其中正确的为________(写出所有判断正确的序号).
科目:高中数学 来源: 题型:
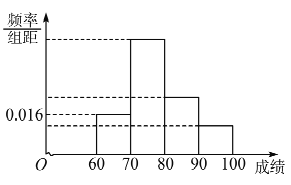
【题目】某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学(成绩得分为整数,满分100分)进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在![]() 的人数为12人.
的人数为12人.
(Ⅰ)求此班级人数;
(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)记甲乙二人排在前三位的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的实轴端点分别为
的实轴端点分别为![]() ,记双曲线的其中一个焦点为
,记双曲线的其中一个焦点为![]() ,一个虚轴端点为
,一个虚轴端点为![]() ,若在线段
,若在线段![]() 上(不含端点)有且仅有两个不同的点
上(不含端点)有且仅有两个不同的点![]() ,使得
,使得![]() ,则双曲线的离心率
,则双曲线的离心率![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时, ![]() ;
;
(1)求函数![]() 在
在![]() 上的解析式并画出函数
上的解析式并画出函数![]() 的图象(不要求列表描点,只要求画出草图)
的图象(不要求列表描点,只要求画出草图)
(2)(ⅰ)写出函数![]() 的单调递增区间;
的单调递增区间;
(ⅱ)若方程![]() 在
在![]() 上有两个不同的实数根,求实数
上有两个不同的实数根,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是双曲线![]()
![]() 左支上一点,
左支上一点, ![]() 是双曲线的左右两个焦点,且
是双曲线的左右两个焦点,且![]() ,线段
,线段![]() 的垂直平分线恰好是该双曲线的一条渐近线,则离心率为( )
的垂直平分线恰好是该双曲线的一条渐近线,则离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 与
与![]() 轴的正半轴相交于点
轴的正半轴相交于点![]() ,点
,点![]() 为椭圆的焦点,且
为椭圆的焦点,且![]() 是边长为2的等边三角形,若直线
是边长为2的等边三角形,若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .
.
(1)直线![]() 的斜率之积是否为定值?若是,请求出该定值;若不是,请说明理由;
的斜率之积是否为定值?若是,请求出该定值;若不是,请说明理由;
(2)求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com