
【题目】如图,已知三棱柱![]() 的侧棱垂直于底面,
的侧棱垂直于底面,![]()
![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)设![]() ,当
,当![]() 为何值时,
为何值时,![]() 平面
平面![]() ,试证明你的结论.
,试证明你的结论.
【答案】(Ⅰ)证明见解析(Ⅱ)![]() 时,
时,![]()
【解析】
试题(1)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(2)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.
试题解析:
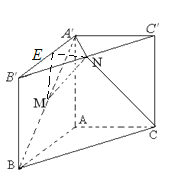
(Ⅰ)取![]() 得中点
得中点![]() ,连接
,连接![]() ,因为
,因为![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点,
所以![]() 又因为
又因为![]() ,
,![]() ,
,
所以![]() ,
,![]() , 5分
, 5分
所以![]() ,因为
,因为![]() ,
,
所以![]() ; 6分
; 6分
(Ⅱ)连接![]() ,设
,设![]() ,则
,则![]() ,
,
由题意知![]()
因为三棱柱![]() 侧棱垂直于底面,
侧棱垂直于底面,
所以![]() ,
,
因为![]() ,点
,点![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
![]() , 9分
, 9分
要使![]() ,
,
只需![]() 即可,
即可,
所以![]() ,即
,即![]() ,
,
则![]() 时,
时,![]() . 12分
. 12分


科目:高中数学 来源: 题型:
【题目】(文)(2017·衡水二模)某商场在元旦举行购物抽奖促销活动,规定顾客从装有编号0,1,2,3,4的五个相同小球的抽奖箱中一次任意摸出两个小球,若取出的两个小球的编号之和等于7则中一等奖,等于6或5则中二等奖,等于4则中三等奖,其余结果为不中奖.
(1)求中二等奖的概率.
(2)求不中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年某市有2万多文科考生参加高考,除去成绩为![]() 分(含
分(含![]() 分)以上的3人与成绩为
分)以上的3人与成绩为![]() 分(不含
分(不含![]() 分)以下的3836人,还有约1.9万文科考生的成绩集中在
分)以下的3836人,还有约1.9万文科考生的成绩集中在![]() 内,其成绩的频率分布如下表所示:
内,其成绩的频率分布如下表所示:
分数段 |
|
|
|
|
频率 | 0.108 | 0.133 | 0.161 | 0.183 |
分数段 |
|
|
|
|
频率 | 0.193 | 0.154 | 0.061 | 0.007 |
(Ⅰ)试估计该次高考成绩在![]() 内文科考生的平均分(精确到
内文科考生的平均分(精确到![]() );
);
(Ⅱ)一考生填报志愿后,得知另外有4名同分数考生也填报了该志愿.若该志愿计划录取3人,并在同分数考生中随机录取,求该考生不被该志愿录取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量, ![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
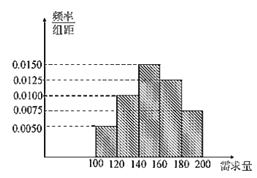
(1)根据直方图估计这个开学季内市场需求量![]() 的平均数;
的平均数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于4000元的概率.
不少于4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]
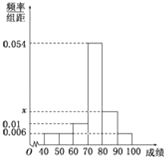
(Ⅰ)求图中![]() 的值,并估计该班期中考试数学成绩的众数;
的值,并估计该班期中考试数学成绩的众数;
(Ⅱ)从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人,求这2人成绩均不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下四种变换方式:
![]() 向左平移
向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ;
;
![]() 向左平移
向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ;
;
![]() 把各点的横坐标缩短到原来的
把各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ,再向左平移
,再向左平移![]() 个单位长度;
个单位长度;
![]() 把各点的横坐标缩短到原来的
把各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ,再向左平移
,再向左平移![]() 个单位长度;
个单位长度;
其中能将函数![]() 的图象变为函数
的图象变为函数![]() 的图象的是
的图象的是![]()
![]()
A. ![]() 和
和![]() B.
B. ![]() 和
和![]() C.
C. ![]() 和
和![]() D.
D. ![]() 和
和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表:
温度x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵个数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
(I)根据散点图判断,![]() 与
与![]() 哪一个适宜作为产卵数
哪一个适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(II)根据(I)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)红铃虫是棉区危害较重的害虫,可从农业、物理和化学三个方面进行防治,其中农业方面防治有3种方法,物理方面防治有1种方法,化学方面防治3种方法,现从7种方法中选3种方法进行综合防治(即3种方法不能全部来自同一方面,至少来自两个方面),X表示在综合防治中农业方面的防治方法的种数,求X的分布列及数学期望E(X).
附:可能用到的公式及数据表中(表中![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() )
)
|
|
|
|
|
|
|
27.430 | 3.612 | 81.290 | 147.700 | 2763.764 | 705.592 | 40.180 |
对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com