

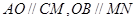 ,再根据线面与面面平行的判定定理证得;
,再根据线面与面面平行的判定定理证得;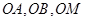 两两垂直,所以以
两两垂直,所以以 为原点建立空间直角坐标系,分别求出面
为原点建立空间直角坐标系,分别求出面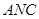 与面
与面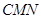 的法向量,利用公式
的法向量,利用公式 ,最后又 图像确定钝角还是锐角;
,最后又 图像确定钝角还是锐角;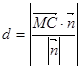 .此题比较容易,难点在求解法向量的计算过程容易出错,所以平时要加大法向量的求解要求.
.此题比较容易,难点在求解法向量的计算过程容易出错,所以平时要加大法向量的求解要求.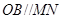 ,
,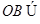 平面
平面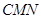
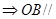 平面
平面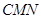
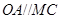 ,
,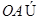 平面
平面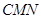
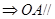 平面
平面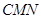
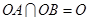 ,∴平面
,∴平面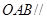 平面
平面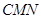 ,又
,又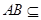 平面
平面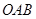 ,
,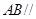 平面
平面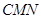 4分
4分 为
为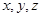 轴建立坐标系,
轴建立坐标系,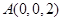 ,
, ,
,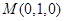 ,
, ,
,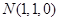 ,
,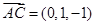 ,
,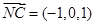 ,设平面
,设平面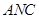 的法向量为
的法向量为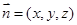 ,
,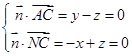 ,令
,令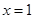 ,得
,得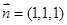 ,而平面
,而平面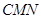 的法向量为:
的法向量为: ,
,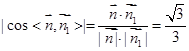 8分
8分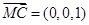 ,由(2)知平面
,由(2)知平面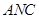 的法向量为:
的法向量为: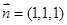 ,
,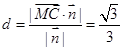 12分
12分

科目:高中数学 来源:不详 题型:填空题
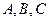 三点在球心为
三点在球心为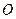 ,半径为
,半径为 的球面上,
的球面上,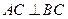 ,且
,且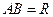 那么
那么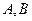 两点的球面距离为_______________,球心到平面
两点的球面距离为_______________,球心到平面 的距离为______________.
的距离为______________.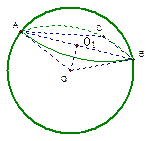
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
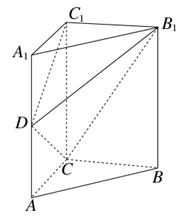
A.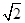 | B.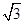 | C.2 | D.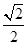 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
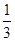 BD,AN=
BD,AN=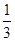 AE.求证:MN∥平面CDE.
AE.求证:MN∥平面CDE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com