
【题目】设![]() 是定义在
是定义在![]() 上的偶函数,
上的偶函数, ![]() ,都有
,都有![]() ,且当
,且当![]() 时,
时, ![]() ,若函数
,若函数![]() (
(![]() )在区间
)在区间![]() 内恰有三个不同零点,则实数
内恰有三个不同零点,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l经过点P(2,0),其倾斜角为,在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为![]() .
.
(Ⅰ)若直线l与曲线C有公共点,求倾斜角的取值范围;
(Ⅱ)设M(x,y)为曲线C上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
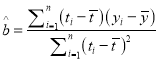 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式.
)的函数解析式.
(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
![]()
以100天记录的各需求量的频率作为各需求量发生的概率.
(1)若花店一天购进17枝玫瑰花, ![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)若花店计划一天购进16枝或17枝玫瑰花,以利润角度看,你认为应购进16枝好还是17枝好?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把长![]() 和宽
和宽![]() 分别为
分别为![]() 和2的长方形
和2的长方形![]() 沿对角线
沿对角线![]() 折成
折成![]() 的二面角
的二面角![]() ,下列正确的命题序号是__________.
,下列正确的命题序号是__________.
①四面体![]() 外接球的体积随
外接球的体积随![]() 的改变而改变;
的改变而改变;
②![]() 的长度随
的长度随![]() 的增大而增大;
的增大而增大;
③当![]() 时,
时,![]() 长度最长;
长度最长;
④当![]() 时,
时,![]() 长度等于
长度等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,四边形
中,四边形![]() 为矩形,四边形
为矩形,四边形![]() 为梯形,
为梯形, ![]() ,平面
,平面![]() 与平面
与平面![]() 垂直,且
垂直,且![]() .
.
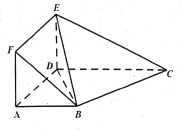
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,且平面
,且平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】无穷数列![]() 满足:
满足: ![]() 为正整数,且对任意正整数
为正整数,且对任意正整数![]() ,
, ![]() 为前
为前![]() 项
项![]() ,
, ![]() ,
, ![]() ,
, ![]() 中等于
中等于![]() 的项的个数.
的项的个数.
(Ⅰ)若![]() ,请写出数列
,请写出数列![]() 的前7项;
的前7项;
(Ⅱ)求证:对于任意正整数![]() ,必存在
,必存在![]() ,使得
,使得![]() ;
;
(Ⅲ)求证:“![]() ”是“存在
”是“存在![]() ,当
,当![]() 时,恒有
时,恒有![]()
![]() 成立”的充要条件。
成立”的充要条件。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com