
����Ŀ��ijũ�����Զ�����ҹ�²��С��ij�����ڴ���Ʒ�ַ�ѿ����֮��Ĺ�ϵ���з����о���12��1����12��5�յ���ҹ�²���ʵ����ÿ��ÿ100�������еķ�ѿ�����±���ʾ��
���� | 12��1�� | 12��2�� | 12��3�� | 12��4�� | 12��5�� |
�²�x(��) | 10 | 11 | 13 | 12 | 8 |
��ѿ��y(��) | 23 | 25 | 30 | 26 | 16 |
��ũ����ȷ�����о������ǣ��ȴ���5��������ѡȡ2�飬��ʣ�µ�3��������ع鷽�̣����ñ�ѡȡ��2�����ݽ��м��飮
(1)��ѡȡ��2������ǡ���Dz����ڵ�2�����ݵĸ��ʣ�
(2)��ѡȡ����12��1����12��5�յ��������ݣ������12��2����12��4�յ����ݣ���y����x�����Իع鷽��![]() .
.
(3)�������Իع鷽�̵õ��Ĺ�����������ѡ���ļ������ݵ�������2�ţ�����Ϊ�õ������Իع鷽���ǿɿ��ģ�����(2)�����õ����Իع鷽���Ƿ�ɿ���
���𰸡���1��![]() �� ��2��
�� ��2��![]() �� ��3��(2)�����õ������Իع鷽���ǿɿ��ģ�.
�� ��3��(2)�����õ������Իع鷽���ǿɿ��ģ�.
��������
��1����鵽������2������Ϊ�¼�A.��Ϊ��5��������ѡȡ2�����ݹ���10����������г鵽����2�����ݵ��������4�֣����ùŵ���͵ĸ��ʼ��㹫ʽ��������⣻
��2�����ù�ʽ����![]() ��ֵ�����
��ֵ�����![]() ������ع鷽�����
������ع鷽�����![]() ��ֵ�����ɵõ��ع�ֱ�ߵķ��̣�
��ֵ�����ɵõ��ع�ֱ�ߵķ��̣�
��3���ֱ���![]() ��
��![]() ������ع�ֱ�ߵķ��̣������Ӧ��
������ع�ֱ�ߵķ��̣������Ӧ��![]() ��ֵ�����������ж�.
��ֵ�����������ж�.
(1)��鵽������2������Ϊ�¼�A.��Ϊ��5��������ѡȡ2�����ݹ���10�������ÿ������ǵȿ��ܳ��ֵģ����г鵽����2�����ݵ��������4�֣�����P(A)��1��![]() ��
��![]() ����ѡȡ��2������ǡ���Dz����ڵ�2�����ݵĸ���Ϊ
����ѡȡ��2������ǡ���Dz����ڵ�2�����ݵĸ���Ϊ![]() .
.
(2)����12��2����12��4�յ����ݣ����x��![]() ��(11��13��12)��12��y��
��(11��13��12)��12��y��![]() ��(25��30��26)��27��
��(25��30��26)��27��
![]() ��
��
![]() ��
��
�ɹ�ʽ���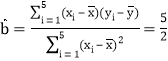 ��
��![]() .
.
����y����x�����Իع鷽��Ϊ![]() ��
��![]() x��3.
x��3.
(3)��x��10ʱ��![]() ��
��![]() x��3��22��|22��23|<2��ͬ���أ���x��8ʱ��
x��3��22��|22��23|<2��ͬ���أ���x��8ʱ��![]() ��
��![]() ��8��3��17��|17��16|<2��
��8��3��17��|17��16|<2��
����(2)�����õ������Իع鷽���ǿɿ��ģ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}�Ĺ���d��0����a1a6=11��a3+a4=12��
��1��������{an}��ͨ�ʽ��
��2��������{ ![]() }��ǰn���Tn ��
}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У��������ǣ� ��
A.x��R��2x��x2
B.��a��b��c��d���� a��c��b��d
C.x��R��ex��0
D.ac2��bc2��a��b�ij�ֲ���Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ұ��ij�ֽ��������þ��豸���������豸��Ϊ�˼������������豸�����IJ�Ʒ���������ʵĹ�ϵ�����������±���ʾ��
���� | ���ʸ� | ���ʵ� |
���豸 | 37 | 121 |
���豸 | 22 | 202 |
�����������ݣ���(����)
A. �����ʵĸߵ����豸�����й�
B. �����ʵĸߵ����豸������
C. �豸�Ƿ������������ʵĸߵ�
D. ���ϴ𰸶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�������У�������������x��y��ͳ�ƽ��������ı���1��ʾ��
x | 1 | 2 | 3 | 4 | 5 |
y | 2 | 3 | 4 | 4 | 5 |
����1

(1)�ڸ���������ϵ�л�������x��y��ɢ��ͼ��
(2)��ȫ����2�����ݱ���2�е����ݺ�ʽ ���������⣮
���������⣮
�����y����x�Ļع�ֱ�߷���![]() �е�
�е�![]() .
.
�ڹ��Ƶ�x��10ʱ��![]() ��ֵ�Ƕ��٣�
��ֵ�Ƕ��٣�
����2
��� | x | y | x2 | xy |
1 | 1 | 2 | 1 | 2 |
2 | 2 | 3 | 4 | 6 |
3 | 3 | 4 | 9 | 12 |
4 | 4 | 4 | 16 | 16 |
5 | 5 | 5 | 25 | 25 |
�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ԲC�� ![]() =1��a��1�������Ҷ���ֱ�ΪA��B��P����ԲC����һ�㣬�ҵ�Pλ�ڵ�һ���ޣ�ֱ��PA��y���ڵ�Q��ֱ��PB��y���ڵ�R������Q����Ϊ��0��1��ʱ����R����Ϊ��0��2��
=1��a��1�������Ҷ���ֱ�ΪA��B��P����ԲC����һ�㣬�ҵ�Pλ�ڵ�һ���ޣ�ֱ��PA��y���ڵ�Q��ֱ��PB��y���ڵ�R������Q����Ϊ��0��1��ʱ����R����Ϊ��0��2�� 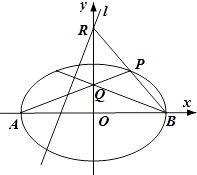
��1������ԲC�ı����̣�
��2����֤�� ![]() Ϊ��ֵ��
Ϊ��ֵ��
��3����֤������R����ֱ��QB��ֱ��ֱ�߾������㣬������ö�������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���� ( )
A. ��x<1������log2(x+1)<1���ij�ֲ���Ҫ����
B. ������x>0��2x>1���ķ�����x0��0��![]() ��1��
��1��
C. ��������a��b����ac2��bc2������������������
D. ��������a+b��5����a��2��b��3�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����P-ABCD��,PA������ABCD,�ı���ABCD��ֱ������,��BAD=��ADC=90��,EΪCB���е�,AB=PA=AD=2CD,��AP��ƽ��PDE���ɽǵ�����ֵΪ ( )
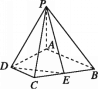
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��{bn}��Ϊ�������ȵ����У�SnΪ{an}��ǰn��ͣ�an+1bn=Sn+1��n��N����
��1����a1=1��bn= ![]() ����a4��ֵ��
����a4��ֵ��
��2����{an}�ǹ���Ϊq�ĵȱ����У���֤������ʵ���ˣ�ʹ��{bn+��}Ϊ�ȱ����У�
��3����{an}�ĸ����Ϊ�㣬{bn}�ǹ���Ϊd�ĵȲ����У���֤��a2 �� a3 �� ����an���ɵȲ����еij�Ҫ������d= ![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com