
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AC⊥BC,E、F分别在线段B1C1和AC上,B1E=3EC1 , AC=BC=CC1=4
(1)求证:BC⊥AC1;
(2)试探究满足EF∥平面A1ABB1的点F的位置,并给出证明.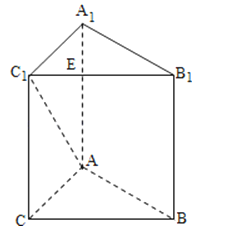
【答案】证明:(1)∵AA1⊥平面ABC,∴AA1⊥BC,
又∵AC⊥BC,AA1∩AC=A,
∴BC⊥平面AA1C1C,
∴BC⊥AC1 .
(2)解法一:当AF=3FC时,EF∥平面AA1B1B.
证明如下:在平A1B1C1内过E作EG∥A1C1交A1B1于G,连接AG.
∵B1E=3EC1 , ∴![]() ,
,
又AF∥A1C1且![]()
∴AF∥EG且AF=EG,
∴四边形AFEG为平行四边形,∴EF∥GA,
又∵EF面AA1B1B,AG平面AA1B1B,
∴EF∥平面AA1B1B.
解法二:当AF=3FC时,FE∥平面A1ABB1 .
证明:在平面ABC内过E作EG∥BB1交BC于G,连接FG.
∵EG∥BB1 , EGA1ABB1 , BB1平面A1ABB1 ,
∴EG∥平面A1ABB1 .
∵B1E=3EC1 , ∴BG=3GC.
∴FG∥AB,
又AB平面A1ABB1 , FG平面A1ABB1 .
∴FG∥平面A1ABB1 .
又EG∩FG=F,
∴平面EFG∥平面A1ABB1 .
∴EF∥平面A1ABB1 . 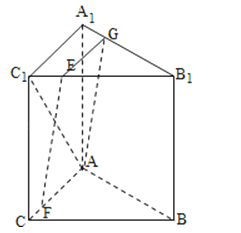
【解析】(1)利用线面垂直的判定定理和性质定理即可证明;
(2)证法一:利用线面平行的判定定理即可证明;证法二:利用面面平行的判定定理.
【考点精析】解答此题的关键在于理解直线与平面平行的性质的相关知识,掌握一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行.


科目:高中数学 来源: 题型:
【题目】如图,正四面体![]() 的顶点
的顶点![]() 分别在两两垂直的三条射线
分别在两两垂直的三条射线![]() 上,在下列命题中,错误的是( )
上,在下列命题中,错误的是( )

A. 四面体![]() 是正三棱锥 B. 直线
是正三棱锥 B. 直线![]() 与平面
与平面![]() 相交 C. 异面直线
相交 C. 异面直线![]() 和
和![]() 所成角是
所成角是![]() D. 直线
D. 直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限
![]() (单位:年,
(单位:年, ![]() )和所支出的维护费用
)和所支出的维护费用![]() (单位:万元)厂家提供的统计资料如下:
(单位:万元)厂家提供的统计资料如下:
使用年限 | 1 | 2 | 3 | 4 | 5 |
维护费用 | 6 | 7 | 7.5 | 8 | 9 |
![]() 请根据以上数据,用最小二乘法原理求出维护费用
请根据以上数据,用最小二乘法原理求出维护费用![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
![]() 若规定当维护费用
若规定当维护费用![]() 超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
参考公式:最小二乘估计线性回归方程![]() 中系数计算公式:
中系数计算公式:
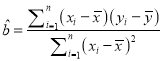 ,
, ![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在棱长为2cm的正方体ABCD﹣A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.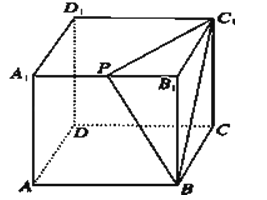
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )

A. ![]() ;
; ![]() B.
B. ![]() ;
; ![]()
C. ![]() ;
; ![]() D.
D. ![]() ;
; ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣ax﹣2a2(x∈R).
(1)关于x的不等式f(x)<0的解集为A,且A[﹣1,2],求a的取值范围;
(2)是否存在实数a,使得当x∈R时, ![]() 成立.若存在给出证明,若不存在说明理由.
成立.若存在给出证明,若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com