解:(I)证明:连接PM,假设直线PM∥平面A′AB
∵PM?平面A′BC,平面A′BC∩平面A′AB=A′B
∴PM∥A′B
又∵M为BC的中点,故P为A′C的中点
∵AA′⊥平面ABC,CC′⊥平面ABC
AA′∥CC′
∴

∴
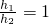
∴h
1=h
2与h
1>h
2矛盾
假设错误,所以直线PM与平面A′AB不平行
(II)(法一)连接BO,则BO⊥AC
∵A′A⊥平面ABC,∴平面A′ACC′⊥平面ABC
∵平面ABC∩平面A′ACC′=AC
∴BO⊥平面A′ACC′
在平面A′ACC′内过O作A′C′的垂线,垂足为D,连接OD,则∠BDO为二面角B-A′C′-A的平面角
∴∠BDO=45°∴△BDO为等腰直角三角形,OD=

∵
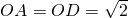
且∠A′AO=∠A′DO=90°
∴Rt△A′AO≌Rt△A′DO∴A′D=2同理得C′D=h
2则由勾股定理可得
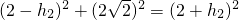
∴h
2=1
又直线OP与平面A′BP所成的角即直线OP与平面A′BC所成的角,设为α,设点O到平面A′BC的距离为h
o,
点P到平面ABC的距离为h
p则
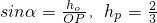
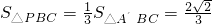
,S
△OBC=1
由等体积法可得
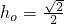
在平面A′ACC′内可求得OP=

,∴
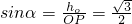
所以直线OP与平面A′BP所成的角为60°.
分析:(I)由要证明的结论的特点,考虑利用反证法:假设直线PM∥平面A′AB可得PM∥A′B,又M为BC的中点,故可得P为A′C的中点,又AA′∥CC
'可得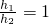
与h
1>h
2矛盾
(II)连接BO,则BO⊥AC由A′A⊥平面ABC可得平面A′ACC′⊥平面ABC,则BO⊥平面A′ACC',在平面A′ACC′内过O作A′C′的垂线,垂足为D,连接OD,则∠BDO为二面角B-A′C′-A的平面角,结合已知条件可求
点评:本题主要考查了利用反证法证明数学命题应用,反证法的关键是要由假设进行逻辑推理,从而得出矛盾,还考查了直线与平面所成的角的求解,解题中要注意利用等体积求解距离的方法的应用.

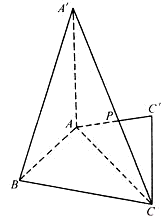 如图,Rt△ABC中,∠ABC=90°,BA=BC=2,分别过A、C作平面ABC的垂线AA′和CC′,AA′=h1,CC′=h2,且h1>h2,连接A′C和AC′交于点P.
如图,Rt△ABC中,∠ABC=90°,BA=BC=2,分别过A、C作平面ABC的垂线AA′和CC′,AA′=h1,CC′=h2,且h1>h2,连接A′C和AC′交于点P. ∴
∴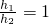

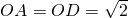 且∠A′AO=∠A′DO=90°
且∠A′AO=∠A′DO=90°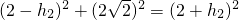 ∴h2=1
∴h2=1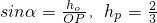
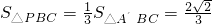 ,S△OBC=1
,S△OBC=1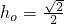
 ,∴
,∴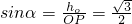
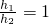 与h1>h2矛盾
与h1>h2矛盾

 如图,Rt△ABC中,∠ABC=90°,BA=BC=2,分别过A、C作平面ABC的垂线AA′和CC′,AA′=h1,CC′=h2,且h1>h2,连接A′C和AC′交于点P.
如图,Rt△ABC中,∠ABC=90°,BA=BC=2,分别过A、C作平面ABC的垂线AA′和CC′,AA′=h1,CC′=h2,且h1>h2,连接A′C和AC′交于点P. (2012•湛江二模)如图,Rt△ABC中,∠C=90°,∠A=30°,圆O经过B、C且与AB、AC分别相交于D、E.若AE=EC=2
(2012•湛江二模)如图,Rt△ABC中,∠C=90°,∠A=30°,圆O经过B、C且与AB、AC分别相交于D、E.若AE=EC=2 如图在Rt△ABC中,三个顶点坐标分别为A(-1,0),B(1,0),C(-1,
如图在Rt△ABC中,三个顶点坐标分别为A(-1,0),B(1,0),C(-1,