
【题目】已知等差数列{an}的前n项和为Sn , 且a2=3,S5=25.
(1)求数列{an}的通项公式an;
(2)设数列{ ![]() }的前n项和为Tn , 是否存在k∈N* , 使得等式2﹣2Tk=
}的前n项和为Tn , 是否存在k∈N* , 使得等式2﹣2Tk= ![]() 成立,若存在,求出k的值;若不存在,说明理由.
成立,若存在,求出k的值;若不存在,说明理由.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
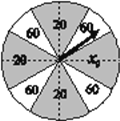
【题目】某大型超市拟对店庆当天购物满![]() 元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.
元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.
(Ⅰ)若![]() ,求顾客转动一次转盘获得
,求顾客转动一次转盘获得![]() 元代金券的概率;
元代金券的概率;
(Ⅱ)某顾客可以连续转动两次转盘并获得相应奖励,当![]() 时,求该顾客第一次获得代金券的面额不低于第二次获得代金券的面额的概率;
时,求该顾客第一次获得代金券的面额不低于第二次获得代金券的面额的概率;
(Ⅲ)记顾客每次转动转盘获得代金券的面额为![]() ,当
,当![]() 取何值时,
取何值时, ![]() 的方差最小?
的方差最小?
(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了丰富学生的业余生活,以班级为单位组织学生开展古诗词背诵比赛,随机抽取题目,背诵正确加10分,背诵错误减10分,只有“正确”和“错误”两种结果,其中某班级的正确率为 ![]() ,背诵错误的概率为
,背诵错误的概率为 ![]() ,现记“该班级完成n首背诵后总得分为Sn”.
,现记“该班级完成n首背诵后总得分为Sn”.
(1)求S6=20且Si≥0(i=1,2,3)的概率;
(2)记ξ=|S5|,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,
中, ![]() 为坐标原点,曲线
为坐标原点,曲线![]() :
: 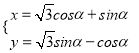 (
(![]() 为参数),在以平面直角坐标系的原点为极点,
为参数),在以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,取相同单位长度的极坐标系,直线
轴的正半轴为极轴,取相同单位长度的极坐标系,直线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)曲线![]() 上恰好存在三个不同的点到直线
上恰好存在三个不同的点到直线![]() 的距离相等,分别求出这三个点的极坐标.
的距离相等,分别求出这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
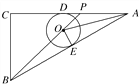
【题目】如图,在△ABC中,∠C=90°,AC=8 cm,AB=10 cm,点P由C出发以每秒2 cm的速度沿线段CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2 s时,⊙O的半径是( )
A. ![]() cm B.
cm B. ![]() cm C.
cm C. ![]() cm D. 2 cm
cm D. 2 cm
查看答案和解析>>
科目:高中数学 来源: 题型:
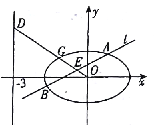
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,如图所示,斜率为
,如图所示,斜率为![]() 且不过原点的直线
且不过原点的直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,射线
,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数 ![]() 的图象,只要将函数y=sin2x的图象( )
的图象,只要将函数y=sin2x的图象( )
A.向右平移 ![]() 个单位长度
个单位长度
B.向左平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com