
| y |
| x |
| 4(-2x2+23x-50) |
| x |
| 25 |
| x |
| 25 |
| x |
x•
|


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源:不详 题型:填空题
 是不相等的两个正数,
是不相等的两个正数, 之间插入两组数:
之间插入两组数: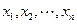 和
和 ,(
,(  ,且
,且 ,使得
,使得
 成等差数列,
成等差数列, 成等比数列.老师给出下列四个式子:①
成等比数列.老师给出下列四个式子:①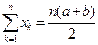 ;②
;② ; ③
; ③ ;④
;④ ;⑤
;⑤ .其中一定成立的是 .
.其中一定成立的是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.1<ab<
| B.ab<1<
| ||||
C.ab<
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1m | B.1.5m | C.0.75m | D.0.5m |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com