
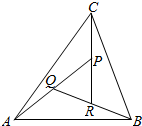
 ��ͼ���ڡ�ABC�У���$\overrightarrow{AB}=\overrightarrow a$��$\overrightarrow{AC}=\overrightarrow b$��AP���е�ΪQ��BQ���е�ΪR��CR���е�ΪP����$\overrightarrow{AP}=m\vec a+n\vec b$����m��n��Ӧ��ֵΪ ��������
��ͼ���ڡ�ABC�У���$\overrightarrow{AB}=\overrightarrow a$��$\overrightarrow{AC}=\overrightarrow b$��AP���е�ΪQ��BQ���е�ΪR��CR���е�ΪP����$\overrightarrow{AP}=m\vec a+n\vec b$����m��n��Ӧ��ֵΪ ��������| A�� | $\frac{2}{7}��\frac{4}{7}$ | B�� | $\frac{1}{2}��\frac{1}{4}$ | C�� | $\frac{1}{6}��\frac{2}{7}$ | D�� | $\frac{1}{6}��\frac{3}{7}$ |
���� �����������������˵ļ���������Եó�$\overrightarrow{BQ}=��\frac{m}{2}-1��\overrightarrow{a}+\frac{n}{2}\overrightarrow{b}$��$\overrightarrow{CR}=��\frac{m}{4}+\frac{1}{2}��\overrightarrow{a}+��\frac{n}{4}-1��\overrightarrow{b}$��������������$\overrightarrow{RQ}��\overrightarrow{QP}��\overrightarrow{RP}$����������$\overrightarrow{RQ}+\overrightarrow{QP}=\overrightarrow{RP}$�����������������������õ�$��\frac{3m}{4}-\frac{1}{2}��\overrightarrow{a}+\frac{3n}{4}\overrightarrow{b}=��-\frac{m}{8}-\frac{1}{4}��\overrightarrow{a}+��\frac{1}{2}-\frac{n}{8}��\overrightarrow{b}$����ƽ�����������������ɽ�������m��n�Ķ�Ԫһ�η����飬�Ӷ����Խ��m��n��
��� �⣺����������$\overrightarrow{BQ}=\overrightarrow{AQ}-\overrightarrow{AB}=\frac{1}{2}\overrightarrow{AP}-\overrightarrow{AB}$=$\frac{1}{2}��m\overrightarrow{a}+n\overrightarrow{b}��-\overrightarrow{a}=��\frac{m}{2}-1��\overrightarrow{a}+\frac{n}{2}\overrightarrow{b}$��
$\overrightarrow{CR}=\overrightarrow{BR}-\overrightarrow{BC}=\frac{1}{2}\overrightarrow{BQ}-\overrightarrow{AC}+\overrightarrow{AB}$=$\frac{1}{2}[��\frac{m}{2}-1��\overrightarrow{a}+\frac{n}{2}\overrightarrow{b}]-\overrightarrow{b}+\overrightarrow{a}$=$��\frac{m}{4}+\frac{1}{2}��\overrightarrow{a}+��\frac{n}{4}-1��\overrightarrow{b}$��
��$\overrightarrow{QP}=\frac{m}{2}\overrightarrow{a}+\frac{n}{2}\overrightarrow{b}$��$\overrightarrow{RQ}=��\frac{m}{4}-\frac{1}{2}��\overrightarrow{a}+\frac{n}{4}\overrightarrow{b}$��$\overrightarrow{RP}=-��\frac{m}{8}+\frac{1}{4}��\overrightarrow{a}+��\frac{1}{2}-\frac{n}{8}��\overrightarrow{b}$��
��$\overrightarrow{RQ}+\overrightarrow{QP}=\overrightarrow{RP}$��
��$��\frac{3m}{4}-\frac{1}{2}��\overrightarrow{a}+\frac{3n}{4}\overrightarrow{b}=��-\frac{m}{8}-\frac{1}{4}��\overrightarrow{a}+��\frac{1}{2}-\frac{n}{8}��\overrightarrow{b}$��
��$\left\{\begin{array}{l}{\frac{3m}{4}-\frac{1}{2}=-\frac{m}{8}-\frac{1}{4}}\\{\frac{3n}{4}=\frac{1}{2}-\frac{n}{8}}\end{array}\right.$��
���$\left\{\begin{array}{l}{m=\frac{2}{7}}\\{n=\frac{4}{7}}\end{array}\right.$��
��ѡ��A��
���� ���������ļӷ��������������˵ļ������壬�Լ��������������㣬ƽ����������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ���� | C�� | �ཻ | D�� | ���ж� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{2}+1}{2}$ | B�� | $\frac{\sqrt{2}-1}{2}$ | C�� | $\frac{\sqrt{3}-1}{4}$ | D�� | $\frac{\sqrt{3}+1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com