
 一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )
一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )| A. | A | B. | B | C. | C | D. | D |
分析 目标函数z=3+ax+by(a,b∈R)可化为:y=$-\frac{a}{b}x-\frac{3}{b}+\frac{z}{b}$由目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,得 $-\frac{a}{b}>{k}_{AB}=\sqrt{3}$,且b<0,a>0.从而得到目标函数变成z=3-bx-ay的最大值只在顶点A处,
解答 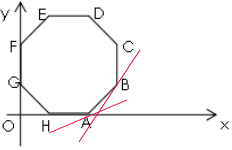 解:目标函数z=3+ax+by(a,b∈R)可化为:y=$-\frac{a}{b}x-\frac{3}{b}+\frac{z}{b}$
解:目标函数z=3+ax+by(a,b∈R)可化为:y=$-\frac{a}{b}x-\frac{3}{b}+\frac{z}{b}$
∵目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,
∴$-\frac{a}{b}>{k}_{AB}=\sqrt{3}$,且b<0,a>0.
目标函数变成z=3-bx-ay可化为y=$-\frac{b}{a}x+\frac{3}{a}-\frac{z}{a}$,
∵$-\frac{b}{a}∈(0,\frac{\sqrt{3}}{3}),\frac{1}{a}<0$,∴目标函数变成z=3-bx-ay时,最大值只在顶点A处,
故选:A
点评 本题考查了线性规划问题,依据直线斜率、纵截距、最优解的范围,确定参数a、b的取值是解题关键,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{3}$,+∞) | B. | ($\frac{1}{3}$,1) | C. | (-∞,-$\frac{1}{3}$) | D. | (-1,-$\frac{1}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com