
【题目】已知函数f(x)=2sin(ωx+φ)﹣1(ω>0,|φ|<π)的一个零点是 ![]() ,
, ![]() 是y=f(x)的图象的一条对称轴,则ω取最小值时,f(x)的单调增区间是( )
是y=f(x)的图象的一条对称轴,则ω取最小值时,f(x)的单调增区间是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:函数f(x)=2sin(ωx+φ)﹣1的一个零点是x= ![]() , ∴f(
, ∴f( ![]() )=2sin(
)=2sin( ![]() ω+φ)﹣1=0,
ω+φ)﹣1=0,
∴sin( ![]() ω+φ)=
ω+φ)= ![]() ,
,
∴ ![]() ω+φ=
ω+φ= ![]() +2kπ或
+2kπ或 ![]() ω+φ=
ω+φ= ![]() +2kπ,k∈Z;
+2kπ,k∈Z;
又直线x=﹣ ![]() 是函数f(x)图象的一条对称轴,
是函数f(x)图象的一条对称轴,
∴﹣ ![]() ω+φ=
ω+φ= ![]() +kπ,k∈Z;
+kπ,k∈Z;
又ω>0,|φ|<π,
∴ω的最小值是 ![]() ,φ=
,φ= ![]() ,
,
∴f(x)=2sin( ![]() x+
x+ ![]() )﹣1;
)﹣1;
令﹣ ![]() +2kπ≤
+2kπ≤ ![]() x+
x+ ![]() ≤
≤ ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
∴﹣ ![]() +3kπ≤x≤﹣
+3kπ≤x≤﹣ ![]() +3kπ,k∈Z;
+3kπ,k∈Z;
∴f(x)的单调增区间是[﹣ ![]() +3kπ,﹣
+3kπ,﹣ ![]() +3kπ],k∈Z.
+3kπ],k∈Z.
故选:B.
【考点精析】解答此题的关键在于理解正弦函数的对称性的相关知识,掌握正弦函数的对称性:对称中心![]() ;对称轴
;对称轴![]() .
.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:高中数学 来源: 题型:
【题目】如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC![]() BC,且AC=BC.
BC,且AC=BC.
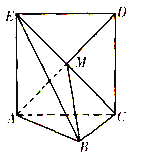
(1)求证:AM![]() 平面EBC;
平面EBC;
(2)求直线AB与平面EBC所成角的大小,
(3)求二面角A-BE-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=e2x , g(x)=kx+1(k∈R). (Ⅰ)若直线y=g(x)和函数y=f(x)的图象相切,求k的值;
(Ⅱ)当k>0时,若存在正实数m,使对任意x∈(0,m),都有|f(x)﹣g(x)|>2x恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线G:y2=2px(p>0),过焦点F的动直线l与抛物线交于A,B两点,线段AB的中点为M.
(Ⅰ)当直线l的倾斜角为 ![]() 时,|AB|=16.求抛物线G的方程;
时,|AB|=16.求抛物线G的方程;
(Ⅱ)对于(Ⅰ)问中的抛物线G,是否存在x轴上一定点N,使得|AB|﹣2|MN|为定值,若存在求出点N的坐标及定值,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A﹣BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE. 
(1)若F是AD的中点,求证:EF∥平面ABC;
(2)若AD=DE,求BE与平面ACE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高速公路为人民出行带来极大便利,但由于高速上车速快,一旦出事故往往导致生命或财产的重大损失,我国高速公路最高限速120km/h,最低限速60km/h.
(1)当驾驶员以120 千米/小时速度驾车行驶,驾驶员发现前方有事故,以原车速行驶大约需要0.9秒后才能做出紧急刹车,做出紧急刹车后,车速依v(t)= ![]() ﹣
﹣ ![]() t(t:秒,v(t):米/秒)规律变化直到完全停止,求驾驶员从发现前方事故到车辆完全停止时,车辆行驶的距离;(取ln5=1.6)
t(t:秒,v(t):米/秒)规律变化直到完全停止,求驾驶员从发现前方事故到车辆完全停止时,车辆行驶的距离;(取ln5=1.6)
(2)国庆期间,高速免小车通行费,某人从襄阳到曾都自驾游,只需承担油费.已知每小时油费v(元)与车速有关,w= ![]() +40(v:km/h),高速路段必须按国家规定限速内行驶,假定高速上为匀速行驶,高速上共行驶了S千米,当高速上行驶的这S千米油费最少时,求速度v应为多少km/h?
+40(v:km/h),高速路段必须按国家规定限速内行驶,假定高速上为匀速行驶,高速上共行驶了S千米,当高速上行驶的这S千米油费最少时,求速度v应为多少km/h?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com