练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设△ABC中，角A，B，C所对的边分别为a，b，c，则“∠C＞90°”的一个充分非必要条件是（　　）
    A.sin2A+sin2B＜sin2C
    B.sinA= ，（A为锐角），cosB=
    C.c2＞2（a+b﹣1）
    D.sinA＜cosB

    【答案】B
    【解析】解：A．若sin2A+sin2B＜sin2C，则a2+b2＜c2，即∠C＞90°为钝角，反之也成立．为充要条件．

    B．若sinA= ，cosB= ，则cosA= ，sinB= ，

    则cosC=﹣cos（A+B）=﹣[cosAcosB﹣sinAsinB]=﹣（ ）= ＜0，则满足条件．

    C．当C=90°时，如a=1，b=2，则c= ，满足c2＞2（a+b﹣1），但此时C=90°，即充分性不成立．

    D．若“∠C＞90°，则“A+B＜90°，即0°＜A＜90°﹣B，

    ∴sinA＜sin（90°﹣B）=cosB，即为充要条件．

    所以答案是：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】王先生家住 A 小区，他工作在 B 科技园区，从家开车到公司上班路上有 L1 ， L2两条路线（如图），L1路线上有 A1 ， A2 ， A3三个路口，各路口遇到红灯的概率均为 ；L2路线上有 B1 ， B2两个路．各路口遇到红灯的概率依次为 ， ．若走 L1路线，王先生最多遇到 1 次红灯的概率为；若走 L2路线，王先生遇到红灯次数 X 的数学期望为 ．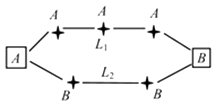

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在下列结论中： ①函数y=sin（kπ﹣x）（k∈Z）为奇函数；
    ②函数 的图象关于点 对称；
    ③函数 的图象的一条对称轴为 π；
    ④若tan（π﹣x）=2，则cos2x= ．
    其中正确结论的序号为（把所有正确结论的序号都填上）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱柱ABCD﹣A1B1C1D1中，AB∥CD，AB1⊥BC，且AA1=AB．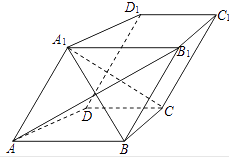

    （1）求证：AB∥平面D1DCC1；
    （2）求证：AB1⊥平面A1BC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知复数z=bi（b∈R）， 是实数，i是虚数单位．
    （1）求复数z；
    （2）若复数（m+z）2所表示的点在第一象限，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a，b，c分别为A，B，C所对边，a+b=4，（2﹣cosA）tan =sinA．
    （1）求边长c的值；
    （2）若E为AB的中点，求线段EC的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线Ω：x2=2py（p＞0），过点（0，2p）的直线与抛物线Ω交于A、B两点，AB的中点为M，若点M到直线y=2x的最小距离为 ，则p=（　　）
    A.
    B.1
    C.
    D.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ln（1+x）﹣ax， ．
    （Ⅰ）当b=1时，求g（x）的最大值；
    （Ⅱ）若对x∈[0，+∞），f（x）≤0恒成立，求a的取值范围；
    （Ⅲ）证明 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系xOy中，椭圆C： 的离心率是 ，
    抛物线E：x2=4y的焦点F是C的一个顶点．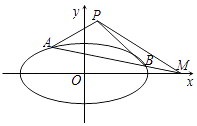

    （1）求椭圆C的方程；
    （2）设与坐标轴不重合的动直线l与C交于不同的两点A和B，与x轴交于点M，且 满足kPA+kPB=2kPM ， 试判断点M是否为定点？若是定点求出点M的坐标；若不是定点请说明理由．

    查看答案和解析>>

    同步练习册答案