练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知定义在R上的可导函数f (x)的导函数为，满足＜f (x)，且f (x＋2)为偶函数，f (4)＝1，则不等式f (x)＜ex的解集为________．

    【答案】

    【解析】

    令，利用导数和已知即可得出其单调性．再利用函数的奇偶性和已知可得g（0）＝1，即可得出．

    令，

    则，

    ∵f′（x）＜f（x），∴g′（x）＜0．

    ∴g（x）在R上单调递减．

    ∵函数f（x+2）是偶函数，

    ∴函数f（﹣x+2）＝f（x+2），

    ∴函数关于x＝2对称，

    ∴f（0）＝f（4）＝1，

    原不等式等价为g（x）＜1，

    ∵g（0）1．

    ∴g（x）＜1g（x）＜g（0），

    ∵g（x）在R上单调递减，

    ∴x＞0．

    ∴不等式f（x）＜ex的解集为（0，+∞）．

    故答案为：（0，+∞）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)及其导数f′(x)，若存在x0，使得f(x0)＝f′(x0)，则称x0是f(x)的一个“巧值点”，则下列函数中有“巧值点”的是________．

    ①f(x)＝x2；②f(x)＝e－x；③f(x)＝lnx；④f(x)＝tanx；⑤.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，ABCD为菱形，∠ABC＝60°，△PAB是边长为2的等边三角形，点M为AB的中点，将△PAB沿AB边折起，使平面PAB⊥平面ABCD，连接PC、PD，如图2，

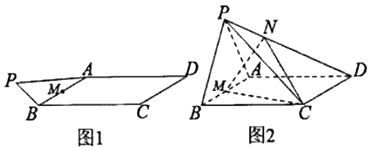
    （1）证明：AB⊥PC；

    （2）求PD与平面ABCD所成角的正弦值

    （3）在线段PD上是否存在点N，使得PB∥平面MC？若存在，请找出N点的位置；若不存在，请说明理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）若，判断函数的奇偶性，并加以证明；

    （2）若函数在上是增函数，求实数的取值范围；

    （3）若存在实数，使得关于的方程有三个不相等的实数根，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商店为了解气温对某产品销售量的影响，随机记录了该商店月份中天的日销售量（单位：千克）与该地当日最低气温（单位：℃）的数据，如表所示：

    （1）求与的回归方程：

    （2）判断与之间是正相关还是负相关；若该地月份某天的最低气温为，请用（1）中的回归方程预测该商店当日的销售量．

    参考公式：，．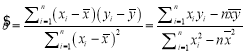

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】判断下列命题的真假并说明理由．

    （1）某个整数不是偶数，则这个数不能被4整除；

    （2）若，且，则，且；

    （3）合数一定是偶数；

    （4）若，则；

    （5）两个三角形两边一对角对应相等，则这两个三角形全等；

    （6）若实系数一元二次方程满足，那么这个方程有两个不相等的实根；

    （7）若集合，，满足，则；

    （8）已知集合，，，如果，那么．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f (x)＝(x－2)ex＋a(x－1)2，讨论f (x)的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某钢管生产车间生产一批钢管，质检员从中抽出若干根对其直径（单位： ）进行测量，得出这批钢管的直径 服从正态分布.

    (1)当质检员随机抽检时，测得一根钢管的直径为,他立即要求停止生产，检查设备，请你根据所学知识，判断该质检员的决定是否有道理，并说明判断的依据；

    (2)如果钢管的直径满足为合格品（合格品的概率精确到0.01），现要从60根该种钢管中任意挑选3根，求次品数的分布列和数学期望.

    （参考数据：若,则； .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为，且，其中.

    （1）求及数列的通项公式；

    （2）若，为整数，且对任意的，恒成立，求的最小值.

    查看答案和解析>>

    同步练习册答案