
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调区间;
的单调区间;
(2)若![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1) 求出函数的导数,通过讨论![]() 的范围,
的范围, ![]() 得增区间,
得增区间, ![]() 得减区间; (2)问题转化为
得减区间; (2)问题转化为![]() ,讨论
,讨论![]() 的范围,根据函数的单调性求出
的范围,根据函数的单调性求出![]() 的最小值即可求出
的最小值即可求出![]() 的范围.
的范围.
试题解析:(1)![]() .
.
(i)当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
(ii)当![]() 时,令
时,令![]() ,则
,则![]() ,
,
当![]() ,即
,即![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() ,即
,即![]() 时,函数
时,函数![]() 单调递减.
单调递减.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(2)令![]() ,由(1)可知,函数
,由(1)可知,函数![]() 的最小值为
的最小值为![]() ,所以
,所以![]() ,即
,即![]() .
.
![]() 恒成立与
恒成立与![]() 恒成立等价,
恒成立等价,
令![]() ,即
,即![]() ,则
,则![]() .
.
①当![]() 时,
时, ![]() .(或令
.(或令![]() ,则
,则
![]() 在
在![]() 上递增,∴
上递增,∴![]() ,∴
,∴![]() 在
在![]() 上递增,∴
上递增,∴![]() .
.
∴![]() ).
).
∴![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() ,
,
∴![]() 恒成立.
恒成立.
②当![]() 时,令
时,令![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增.
单调递增.
又![]() ,
, ![]() ,
,
∴存在![]() ,使得
,使得![]() ,故当
,故当![]() 时,
时, ![]() ,即
,即![]() ,故函数
,故函数![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时, ![]() ,即
,即![]() ,故函数
,故函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
即![]() ,
, ![]() 不恒成立,
不恒成立,
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且该圆存在两点关于直线
上,且该圆存在两点关于直线![]() 对称,又圆
对称,又圆![]() 与直线
与直线![]() 相切,过点
相切,过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点,![]() 是
是![]() 的中点,直线
的中点,直线![]() 与
与![]() 相交于点
相交于点![]() .
.
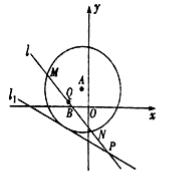
(1)求圆![]() 的方程;
的方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)![]() 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
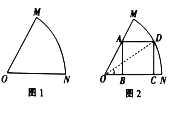
【题目】某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板![]() ,其中顶点
,其中顶点![]() 、
、![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在
在![]() 上,
上, ![]() ,
, ![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
(1)用含![]() 的式子表示
的式子表示![]() ,
, ![]() 的长;
的长;
(2)试将![]() 表示为
表示为![]() 的函数;
的函数;
(3)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 满足:①圆心在第一象限,截
满足:①圆心在第一象限,截![]() 轴所得弦长为2;②被
轴所得弦长为2;②被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() ;③圆心到直线
;③圆心到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 分别做圆
分别做圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
![]() 为定义在
为定义在![]() 上的“局部奇函数”;
上的“局部奇函数”;
![]() 曲线
曲线![]() 与
与![]() 轴交于不同的两点;
轴交于不同的两点;
若![]() 为假命题,
为假命题, ![]() 为真命题,求
为真命题,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有5张编号依次为1、2、3、4、5的卡片,这5 张卡片除号码外完全相同.现进行有放回的连续抽取2 次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求事件“取出卡片号码之和不小于7 或小于5”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com