
【题目】如图,边长为2的正方形ABCD中, 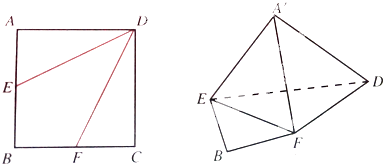
(1)点E是AB的中点,点F是BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.求证:A′D⊥EF
(2)当BE=BF= ![]() BC时,求三棱锥A′﹣EFD的体积.
BC时,求三棱锥A′﹣EFD的体积.
【答案】
(1)解:由正方形ABCD知,∠DCF=∠DAE=90°,
∴A'D⊥A'F,A'D⊥A'E,
∵A'E∩A'F=A',A'E、A'F平面A'EF.
∴A'D⊥平面A'EF.
又∵EF平面A'EF,
∴A'D⊥EF.
(2)解:由四边形ABCD为边长为2的正方形
故折叠后A′D=2,A′E=A′F= ![]() ,EF=
,EF= ![]()
则cos∠EA′F= 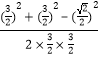 =
= ![]()
则sin∠EA′F= ![]()
故△EA′F的面积S△EA′F= ![]() A′EA′Fsin∠EA′F=
A′EA′Fsin∠EA′F= ![]()
由(1)中A′D⊥平面A′EF
可得三棱锥A'﹣EFD的体积V= ![]() ×
× ![]() ×2=
×2= ![]()
【解析】(1)由正方形ABCD知∠DCF=∠DAE=90°,得A'D⊥A'F且A'D⊥A'E,所以A'D⊥平面A'EF.结合EF平面A'EF,得A'D⊥EF;(2)由勾股定理的逆定理,得△A'EF是以EF为斜边的直角三角形,而A'D是三棱锥D﹣A'EF的高线,可以算出三棱锥D﹣A'EF的体积,即为三棱锥A'﹣DEF的体积.
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点,需要掌握垂直于同一个平面的两条直线平行才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知双曲线![]() ,抛物线
,抛物线![]() ,
, ![]() 与
与![]() 有公共的焦点
有公共的焦点![]() ,
, ![]() 与
与![]() 在第一象限的公共点为
在第一象限的公共点为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,且
,且![]() ,则关于双曲线的离心率的说法正确的是()
,则关于双曲线的离心率的说法正确的是()
A. 仅有两个不同的离心率![]() 且
且![]() B. 仅有两个不同的离心率
B. 仅有两个不同的离心率![]() 且
且![]() C. 仅有一个离心率
C. 仅有一个离心率![]() 且
且![]() D. 仅有一个离心率
D. 仅有一个离心率![]() 且
且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在y=2x2上有一点P,它到A(1,3)的距离与它到焦点的距离之和最小,则点P的坐标是( )
A.(﹣2,1)
B.(1,2)
C.(2,1)
D.(﹣1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
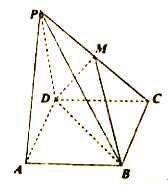
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在
在![]() 上,且满足
上,且满足![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于平面向量,有下列四个命题:
①若 ![]() .
.
② ![]() =(1,1),
=(1,1), ![]() =(2,x),若
=(2,x),若 ![]() 与
与 ![]() 平行,则x=2.
平行,则x=2.
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,则
|,则 ![]() 与
与 ![]() 的夹角为60°.
的夹角为60°.
④点A(1,3),B(4,﹣1),与向量 ![]() 同方向的单位向量为(
同方向的单位向量为( ![]() ).
).
其中真命题的序号为 . (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知向量 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),
), ![]() =(sinx,cosx),x∈(0,
=(sinx,cosx),x∈(0, ![]() ).
).
(1)若 ![]() ⊥
⊥ ![]() ,求tanx的值;
,求tanx的值;
(2)若 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() ,求x的值.
,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com