
【题目】方程![]() 的曲线即为函数
的曲线即为函数![]() 的图象,对于函数
的图象,对于函数![]() ,有如下结论:①
,有如下结论:①![]() 在
在![]() 上单调递减;②函数
上单调递减;②函数![]() 存在零点;③函数
存在零点;③函数![]() 的值域是R;④若函数
的值域是R;④若函数![]() 和
和![]() 的图象关于原点对称,则函数
的图象关于原点对称,则函数![]() 的图象就是
的图象就是![]() 确定的曲线
确定的曲线
其中所有正确的命题序号是________.
【答案】①③
【解析】
根据绝对值的定义去绝对值,将方程![]() 化简,得到相应函数在各区间上的表达式,由此作出图象,即可即可判断各命题的真假.
化简,得到相应函数在各区间上的表达式,由此作出图象,即可即可判断各命题的真假.
当![]() 且
且![]() 时,方程为
时,方程为![]() ,此时方程不成立;
,此时方程不成立;
当![]() 且
且![]() 时,方程为
时,方程为![]() ,即
,即![]() ,
,
当![]() 且
且![]() 时,方程为
时,方程为![]() ,即
,即![]() ,
,
当![]() 且
且![]() 时,方程为
时,方程为![]() ,即
,即![]() ,
,
作出函数的图象,如图所示:

对于①,由图可知,函数在![]() 上单调递减,所以①正确;
上单调递减,所以①正确;
对于②,由![]() 得,
得,![]() ,因为双曲线
,因为双曲线![]() 和
和![]() 的渐近线为
的渐近线为![]() ,所以函数
,所以函数![]() 的图象与直线
的图象与直线![]() 无公共点,因此,函数
无公共点,因此,函数![]() 不存在零点,所以②错误;
不存在零点,所以②错误;
对于③,由图可知,函数![]() 的值域是R,所以③正确;
的值域是R,所以③正确;
对于④,若函数![]() 和
和![]() 的图象关于原点对称,则用
的图象关于原点对称,则用![]() 分别替换
分别替换![]() 可得,
可得,
![]() 即
即![]() ,则函数
,则函数![]() 的图象是
的图象是![]() 确定的曲线,而不是
确定的曲线,而不是![]() 确定的曲线,所以④错误.
确定的曲线,所以④错误.
综上,正确的为①③.
故答案为:①③.


科目:高中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() :
:![]() 的左、右焦点,过
的左、右焦点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 所得弦长为
所得弦长为![]() ,设
,设![]() 、
、![]() 是椭圆
是椭圆![]() 上的两个动点,线段
上的两个动点,线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 的横坐标为1.
的横坐标为1.
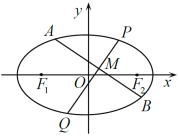
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的左、右焦点为
)的左、右焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .已知
.已知![]() .
.
(1)求椭圆的离心率;
(2)设![]() 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,经过原点
,经过原点![]() 的直线
的直线![]() 与该圆相切,求直线
与该圆相切,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() .
.
(Ⅰ)若![]() .
.
(i)求椭圆![]() 的离心率;
的离心率;
(ii)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,若
,若![]() 的面积为
的面积为![]() ,求椭圆
,求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)由椭圆![]() 上不同三点构成的三角形称为椭圆的内接三角形,当
上不同三点构成的三角形称为椭圆的内接三角形,当![]() 时,若以
时,若以![]() 为直角顶点的椭圆
为直角顶点的椭圆![]() 的内接等腰直角三角形恰有3个,求实数
的内接等腰直角三角形恰有3个,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() :
:![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的任意一点,射线
上的任意一点,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,直线
有且只有一个公共点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两个相异点,证明:
两个相异点,证明:![]() 面积为定值.
面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).
阶梯级别 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用电范围(度) | (0,210] | (210,400] |
|
某市随机抽取10户同一个月的用电情况,得到统计表如下:
居民用电户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用电量(度) | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯的部分每度0.8元,试计算A居民用电户用电410度时应电费多少元?
现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
以表中抽到的10户作为样本估计全市的居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某绿色有机水果店中一款有机草莓味道鲜甜,店家每天以每斤![]() 元的价格从农场购进适量草莓,然后以每斤
元的价格从农场购进适量草莓,然后以每斤![]() 元的价格出售,如果当天卖不完,剩下的草莓由果汁厂以每斤
元的价格出售,如果当天卖不完,剩下的草莓由果汁厂以每斤![]() 元的价格回收.
元的价格回收.
(1)若水果店一天购进![]() 斤草莓,求当天的利润
斤草莓,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:斤,
(单位:斤,![]() )的函数解析式;
)的函数解析式;
(2)水果店记录了![]() 天草莓的日需求量(单位:斤),整理得下表:
天草莓的日需求量(单位:斤),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 14 | 22 | 14 | 16 | 15 | 13 | 6 |
①假设水果店在这![]() 天内每天购进
天内每天购进![]() 斤草莓,求这
斤草莓,求这![]() 天的日利润(单位:元)的平均数;
天的日利润(单位:元)的平均数;
②若水果店一天购进![]() 斤草莓,以
斤草莓,以![]() 天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于
天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于![]() 元的概率.
元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com