
【题目】若函数f(x)=lnx+ax2﹣(a+2)x在 ![]() 处取得极大值,则正数a的取值范围是 .
处取得极大值,则正数a的取值范围是 .
【答案】(0,2)
【解析】解:f(x)的定义域是(0,+∞),
f′(x)= ![]() +2ax﹣(a+2)=
+2ax﹣(a+2)= ![]() ,
,
①a≤0时,ax﹣1<0,
令f′(x)>0,解得:x> ![]() ,令f′(x)<0,解得:0<x<
,令f′(x)<0,解得:0<x< ![]() ,
,
故 ![]() 是函数的极小值点,不合题意,
是函数的极小值点,不合题意,
②0<a<2时, ![]() <
< ![]() ,
,
令f′(x)>0,解得:x< ![]() 或x>
或x> ![]() ,
,
令f′(x)<0,解得: ![]() <x<
<x< ![]() ,
,
∴f(x)在(0, ![]() )递增,在(
)递增,在( ![]() ,
, ![]() )递减,在(
)递减,在( ![]() ,+∞)递增,
,+∞)递增,
∴函数f(x)在 ![]() 处取得极大值,符合题意,
处取得极大值,符合题意,
③a=2时,f′(x)≥0,f(x)递增,无极值,
④a>2时, ![]() >
> ![]() ,
,
令f′(x)>0,解得:x> ![]() 或x<
或x< ![]() ,
,
令f′(x)<0,解得: ![]() <x<
<x< ![]() ,
,
∴f(x)在(0, ![]() )递增,在(
)递增,在( ![]() ,
, ![]() )递减,在(
)递减,在( ![]() ,+∞)递增,
,+∞)递增,
∴函数f(x)在x= ![]() 处取得极大值,不符合题意,
处取得极大值,不符合题意,
综上,a∈(0,2),
所以答案是:(0,2).
【考点精析】掌握函数的极值与导数是解答本题的根本,需要知道求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A′B′C′D′中,E是棱BC的中点,G是棱DD′的中点,则异面直线GB与B′E所成的角为( ) 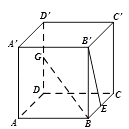
A.120°
B.90°
C.60°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某高级中学学生的体重状况,打算抽取一个容量为n的样本,已知该校高一、高二、高三学生的数量之比依次为4:3:2,现用分层抽样的方法抽出的样本中高三学生有10人,那么样本容量n为( )
A.50
B.45
C.40
D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的方程为
的方程为![]() .
.
(1)以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,求
轴正半轴为极轴建立极坐标系,求![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() 两点,
两点, ![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农户准备建一个水平放置的直四棱柱形储水器(如图),其中直四棱柱的高![]() ,两底面
,两底面![]() 是高为
是高为![]() ,面积为
,面积为![]() 的等腰梯形,且
的等腰梯形,且![]() ,若储水窖顶盖每平方米的造价为100元,侧面每平方米的造价为400元,底部每平方米的造价为500元.
,若储水窖顶盖每平方米的造价为100元,侧面每平方米的造价为400元,底部每平方米的造价为500元.


(1)试将储水窖的造价![]() 表示为
表示为![]() 的函数;
的函数;
(2)该农户如何设计储水窖,才能使得储水窖的造价最低,最低造价是多少元?(取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cosx,
=(2cosx, ![]() sinx),
sinx), ![]() =(3cosx,﹣2cosx),设函数f(x)=
=(3cosx,﹣2cosx),设函数f(x)= ![]()
![]()
(1)求f(x)的最小正周期;
(2)若x∈[0, ![]() ],求f(x)的值域.
],求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a2=5,a5+a7=26,数列{an}的前n项和为Sn .
(1)求an及Sn;
(2)设{bn﹣an}是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,CA=CB,M,N,P分别为AB,A1C1 , BC的中点. 
求证:
(1)C1P∥平面MNC;
(2)平面MNC⊥平面ABB1A1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com