
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 在
在![]() 处取得极值,对
处取得极值,对![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 当![]() 时,
时, ![]() 的单调递减区间是
的单调递减区间是![]() ,无单调递增区间;当
,无单调递增区间;当![]() 时,
时, ![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() (2)
(2) ![]()
【解析】试题分析:(1)![]() 对a分类讨论确定函数
对a分类讨论确定函数![]() 的单调区间;(2)由函数
的单调区间;(2)由函数![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() ,对
,对![]() ,
, ![]() 恒成立即
恒成立即![]() 对
对![]() 恒成立,构造新函数求最值即可.
恒成立,构造新函数求最值即可.
试题解析:
(1)①在区间![]() 上,
上, ![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 在区间
在区间![]() 上单调递减;
上单调递减;
当![]() 时,令
时,令![]() 得
得![]() ,在区间
,在区间![]() 上,
上,
![]() ,函数
,函数![]() 单调递减,在区间
单调递减,在区间![]() 上,
上,
![]() ,函数
,函数![]() 单调递增.
单调递增.
综上所述:当![]() 时,
时, ![]() 的单调递减区间是
的单调递减区间是![]() ,无单调递增区间;
,无单调递增区间;
当![]() 时,
时, ![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]()
②因为函数![]() 在
在![]() 处取得极值,
处取得极值,
所以![]() ,解得
,解得![]() ,经检验可知满足题意.
,经检验可知满足题意.
由已知![]() ,即
,即![]() ,
,
即![]() 对
对![]() 恒成立,
恒成立,
令![]() ,
,
则![]() ,
,
易得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】若1路、2路公交车均途经泉港一中校门口,其中1路公交车每10分钟一趟,2路公交车每20分钟一趟,某生去坐这2趟公交车回家,则等车不超过5分钟的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是一个类似计步数据库的公众帐号,用户只需以运动手环或手机协处理器的运动教据为介,然后关注该公众号,就能看见自己与好友每日行走的步数,并在同一排行榜上得以体现,现随机选取朋友圈中的50人记录了他们某一天的走路步数,并将数据整理如下:

规定:人一天行走的步数超过8000步时被系统评定为“积极性”,否则为“懈怠性”.
(1)填写下面列联表(单位:人),并根据列联表判断是否有![]() 的把握认为“评定类型与性别有关”;
的把握认为“评定类型与性别有关”;

附:
|
|
|
|
|
|
|
|
|
|
|
|

(2)为了进一步了解“懈怠性”人群中每个人的生活习惯,从步行在![]() 的人群中再随机抽取3人,求选中的人中男性人数超过女性人数的概率.
的人群中再随机抽取3人,求选中的人中男性人数超过女性人数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩在进行整理后分成5组,绘制出如图所示的须率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.

(1)求成绩在50-70分的频率是多少
(2)求这三个年级参赛学生的总人数是多少:
(3)求成绩在80-100分的学生人数是多少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级50名学生参加数学竞赛,根据他们的成绩绘制了如图所示的频率分布直方图,已知分数在![]() 的矩形面积为
的矩形面积为![]() ,
,
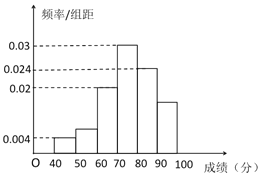
求:![]() 分数在
分数在![]() 的学生人数;
的学生人数;
![]() 这50名学生成绩的中位数
这50名学生成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 若分数高于60分就能进入复赛,从不能进入复赛的学生中随机抽取两名,求两人来自不同组的概率.
若分数高于60分就能进入复赛,从不能进入复赛的学生中随机抽取两名,求两人来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B.
(Ⅰ)若∠APB=60°,试求点P的坐标;
(Ⅱ)若P点的坐标为(2,1),过P作直线与圆M交于C,D两点,当CD=![]() 时,求直线CD的方程.
时,求直线CD的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A、B、C、D的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),![]() ,α∈(
,α∈(![]() ,
,![]() ).
).
(1)若![]() ,求角α的值;
,求角α的值;
(2)若![]() ,求
,求![]() 的值.
的值.
(3)若![]() 在定义域α∈(
在定义域α∈(![]() ,
,![]() )有最小值
)有最小值![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品![]() 和产品
和产品![]() 需要甲、乙两种新型材料.生产一件产品
需要甲、乙两种新型材料.生产一件产品![]() 需要甲材料
需要甲材料![]() ,乙材料
,乙材料![]() ,并且需要花费1天时间;生产一件产品
,并且需要花费1天时间;生产一件产品![]() 需要甲材料
需要甲材料![]() ,乙材料
,乙材料![]() ,也需要1天时间,生产一件产品
,也需要1天时间,生产一件产品![]() 的利润为1000元,生产一件产品
的利润为1000元,生产一件产品![]() 的利润为2000元.该企业现有甲、乙材料各
的利润为2000元.该企业现有甲、乙材料各![]() ,则在不超过120天的条件下,求生产产品
,则在不超过120天的条件下,求生产产品![]() 、产品
、产品![]() 的利润之和的最大值.
的利润之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:极坐标与参数方程
在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数) 上任意一点
为参数) 上任意一点![]() 经过伸缩变换
经过伸缩变换 后得到曲线
后得到曲线![]() 的图形.以坐标原点
的图形.以坐标原点![]() 为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线
为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(Ⅱ)点P为曲线![]() 上的任意一点,求点P到直线
上的任意一点,求点P到直线![]() 的距离的最大值及取得最大值时点P的坐标.
的距离的最大值及取得最大值时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com